| Exercise
4.1 Exercise 4.2 Exercise 4.3 Exercise 4.4 |
Exercise 4.1
Question 1
(i) sin C
(ii) sin A
(iii) cos C
(iv) cos A
(v) tan C
(vi) tan A
Sol :
(i) Sin C
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
So, here θ = C
Side opposite to ∠C = AB = 3
Hypotenuse = AC = 5
So, $\sin C=\frac{A B}{A C}=\frac{3}{5}$
So, here θ = A
The side opposite to ∠A = BC = 4
Hypotenuse = AC = 5
So, $\sin A=\frac{B C}{A C}=\frac{4}{5}$
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
So, here θ = C
Side adjacent to ∠C = BC = 4
Hypotenuse = AC = 5
So, $\cos C=\frac{B C}{A C}=\frac{4}{5}$
Here, θ = A
Side adjacent to ∠A = AB = 3
Hypotenuse = AC = 5
So, $\cos A=\frac{A B}{A C}=\frac{3}{5}$
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
So, here θ = C
Side opposite to ∠C = AB = 3
Side adjacent to ∠C = BC = 4
So, $\tan C=\frac{A B}{B C}=\frac{3}{4}$
here θ = A
Side opposite to ∠A = BC = 4
Side adjacent to ∠A = AB = 3
So, $\tan A=\frac{A B}{B C}=\frac{4}{3}$
Question 2
(ii) cos θ
Sol :
(i) tan θ
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Side opposite to θ = AB = 4
Side adjacent to θ = BC = 3
So, $\tan \theta=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{4}{3}$
(ii) cos θ
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to θ = BC = 3
Hypotenuse = AC = 5
So, $\cos \theta=\frac{B C}{A C}=\frac{3}{5}$
Question 3
(ii) tan θ
(iii) tan A – cot C
(i) sin θ
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to θ = BC = ?
Hypotenuse = AC = 13
Firstly we have to find the value of BC.
So, we can find the value of BC with the help of Pythagoras theorem.
According to Pythagoras theorem,
(Hypotenuse)2 = (Base)2 + (Perpendicular)2
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (12)2 + (BC)2 = (13)2
⇒ 144 + (BC)2 = 169
⇒ (BC)2 = 169–144
⇒ (BC)2 = 25
⇒ BC =√25
⇒ BC =±5
But side BC can’t be negative. So, BC = 5
Now, BC = 5 and AC = 13
So, $\sin \theta=\frac{B C}{A C}=\frac{5}{13}$
(ii) tan θ
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Side opposite to θ = BC = 5
Side adjacent to θ = AB = 12
So, $\tan \theta=\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{5}{12}$
(iii) tan A – cot C
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
and
$\cot \theta=\frac{\text { side adjacent to angle } \theta}{\text { side opposite to angle } \theta}$
tan A
Here, θ = A
Side opposite to ∠A = BC = 5
Side adjacent to ∠A = AB = 12
So, $\tan \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{5}{12}$
Cot C
Here, θ = C
Side adjacent to ∠C = BC = 5
Side opposite to ∠C = AB = 12
So, $\cot C=\frac{B C}{A B}=\frac{5}{12}$
So, $\tan A-\cot C=\frac{5}{12}-\frac{5}{12}=0$
Question 4 A
b. sin C, cos C
Sol :
(a) sin A
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
So, here θ = A
Side opposite to ∠A = BC = 7
Hypotenuse = AC = ?
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem.
(Hypotenuse)2 = (Base)2 + (Perpendicular)2
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (24)2 + (7)2 = (AC)2
⇒ 576 + 49 = (AC)2
⇒ (AC)2 = 625
⇒ AC =√625
⇒ AC =±25
But side AC can’t be negative. So, AC = 25cm
Now, BC = 7 and AC = 25
So, $\sin A=\frac{B C}{A C}=\frac{7}{25}$
Cos A
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
So, here θ = A
Side adjacent to ∠A = AB = 24
Hypotenuse = AC = 25
So,$\cos A=\frac{A B}{A C}=\frac{24}{25}$
(b) sin C
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
So, here θ = C
The side opposite to ∠C = AB = 24
Hypotenuse = AC = 25
So, $\sin C=\frac{A B}{A C}=\frac{24}{25}$
Cos C
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
So, here θ = C
Side adjacent to ∠C = BC = 7
Hypotenuse = AC = 25
So, $\cos C=\frac{B C}{A C}=\frac{7}{25}$
Question 4 B
Consider ∆ACB, right
angled at C, in which AB = 29 units, BC = 21 units and ∠ABC=θ. Determine the values
ofa. cos2 θ+ sin2 θ
b.
cos2 θ – sin2 θ
Sol :
(a) Cos2θ
+sin2 θ
Firstly we have to find the value of
AC.
So, we can find the value of AC with the help of Pythagoras
theorem.
According to Pythagoras theorem,
(Hypotenuse)2 = (Base)2 +
(Perpendicular)2
⇒ (AC)2 + (BC)2 = (AB)2
⇒ (AC)2 + (21)2 =
(29)2
⇒ (AC)2 =
(29)2 – (21)2
Using the identity
a2 –b2 = (a+b) (a – b)
⇒ (AC)2 = (29–21)(29+21)
⇒ (AC)2 = (8)(50)
⇒ (AC)2 = 400
⇒ AC
=√400
⇒ AC =±20
But side
AC can’t be negative. So, AC = 20units
Now, we will find the sin θ and cos
θ
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
In ∆ACB, Side opposite to angle θ =
AC = 20
and Hypotenuse = AB = 29
So, $\sin \theta=\frac{A C}{A B}=\frac{20}{29}$
Now, We know
that
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
In ∆ACB, Side adjacent to
angle θ = BC = 21
and Hypotenuse = AB =
29
So, $\cos \theta=\frac{B C}{A B}=\frac{21}{29}$
So$\cos ^{2} \theta+\sin ^{2}
\theta=\left(\frac{21}{29}\right)^{2}+\left(\frac{20}{29}\right)^{2}$
$=\frac{441+400}{29 \times
29}$
$=\frac{841}{841}$
=1
Cos2θ +sin2 θ = 1
(b) Cos2θ – sin2 θ
Putting values, we get
$\cos ^{2} \theta-\sin ^{2}
\theta=\left(\frac{21}{29}\right)^{2}-\left(\frac{20}{29}\right)^{2}$
$=\frac{441-400}{29 \times
29}$
$=\frac{41}{841}$
b. cos2 θ – sin2 θ
Sol :
(a) Cos2θ +sin2 θ
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem.
According to Pythagoras theorem,
(Hypotenuse)2 = (Base)2 + (Perpendicular)2
⇒ (AC)2 + (BC)2 = (AB)2
⇒ (AC)2 + (21)2 = (29)2
⇒ (AC)2 = (29)2 – (21)2
Using the identity a2 –b2 = (a+b) (a – b)
⇒ (AC)2 = (29–21)(29+21)
⇒ (AC)2 = (8)(50)
⇒ (AC)2 = 400
⇒ AC =√400
⇒ AC =±20
But side AC can’t be negative. So, AC = 20units
Now, we will find the sin θ and cos θ
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
In ∆ACB, Side opposite to angle θ = AC = 20
and Hypotenuse = AB = 29
So, $\sin \theta=\frac{A C}{A B}=\frac{20}{29}$
Now, We know that
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
and Hypotenuse = AB = 29
So, $\cos \theta=\frac{B C}{A B}=\frac{21}{29}$
So$\cos ^{2} \theta+\sin ^{2} \theta=\left(\frac{21}{29}\right)^{2}+\left(\frac{20}{29}\right)^{2}$
$=\frac{441+400}{29 \times 29}$
$=\frac{841}{841}$
=1
Cos2θ +sin2 θ = 1
(b) Cos2θ – sin2 θ
Putting values, we get
$\cos ^{2} \theta-\sin ^{2} \theta=\left(\frac{21}{29}\right)^{2}-\left(\frac{20}{29}\right)^{2}$
$=\frac{441-400}{29 \times 29}$
$=\frac{41}{841}$
Question 4 C
In ∆ABC, ∠A is a right angle, then find the values of sin B, cos C and tan B in each of the following
:a. AB = 12, AC = 5, BC =
13
b. AB = 20, AC = 21, BC =
29
c. BC = √2, AB = AC =
1
Sol :
Given that ∠A is a right angle.
(a) AB = 12, AC = 5, BC = 13
To Find : sin B, cos C and tan B
We know that,
$\sin
\theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Here, θ = B
Side opposite to angle B
= AC = 5
Hypotenuse = BC =13
So, $\sin
\mathrm{B}=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{5}{13}$
Now, Cos C
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text {
hypotenuse }}$
Here, θ = C
Side adjacent to angle C = AC = 5
Hypotenuse = BC
=13
So, $\cos C=\frac{A C}{B C}=\frac{5}{13}$
Now, tan B
We know that,
$\tan \theta=\frac{\text { side
opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Here, θ = B
The
side opposite to angle B = AC = 5
The
side adjacent to angle B = AB = 12
So, $\tan \mathrm{B}=\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{5}{12}$
(b) AB = 20, AC = 21, BC = 29
To Find: sin B, cos C and tan
B
We know that,
$\sin \theta=\frac{\text { side opposite to angle }
\theta}{\text { hypotenuse }}$
Here, θ =
B
The side opposite to angle B = AC
=21
Hypotenuse = BC =29
So, $\sin
B=\frac{A C}{B C}=\frac{21}{29}$
Now, Cos C
We know
that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Here, θ = C
Side adjacent to angle C
= AC = 21
Hypotenuse = BC = 29
So,$\cos C=\frac{A
C}{B C}=\frac{21}{29}$
Now, tan B
We know
that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle }
\theta}$
Here, θ = B
The
side opposite to angle B = AC = 21
The
side adjacent to angle B = AB = 20
So, $\tan \mathrm{B}=\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{21}{20}$
(c) BC =√2, AB = AC = 1
To Find: sin B, cos C and tan B
We know that,
$\sin
\theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Here, θ = B
The
side opposite to angle B = AC =1
Hypotenuse = BC
=√2
So$\sin
\mathrm{B}=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{1}{\sqrt{2}}$
Now, Cos
C
We know that,
$\cos \theta=\frac{\text { side adjacent to angle }
\theta}{\text { hypotenuse }}$
Here, θ =
C
Side adjacent to angle C = AC = 1
Hypotenuse =
BC = √2
So, $\cos C=\frac{A C}{B
C}=\frac{1}{\sqrt{2}}$
Now, tan B
We know
that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle }
\theta}$
Here, θ = B
The
side opposite to angle B = AC = 1
The
side adjacent to angle B = AB = 1
So,$\tan
B=\frac{A C}{A B}=\frac{1}{1}=1$
b. AB = 20, AC = 21, BC = 29
c. BC = √2, AB = AC = 1
Sol :
Given that ∠A is a right angle.
To Find : sin B, cos C and tan B
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Here, θ = B
Side opposite to angle B = AC = 5
Hypotenuse = BC =13
So, $\sin \mathrm{B}=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{5}{13}$
Now, Cos C
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Here, θ = C
Side adjacent to angle C = AC = 5
Hypotenuse = BC =13
So, $\cos C=\frac{A C}{B C}=\frac{5}{13}$
Now, tan B
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Here, θ = B
The side opposite to angle B = AC = 5
The side adjacent to angle B = AB = 12
So, $\tan \mathrm{B}=\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{5}{12}$
(b) AB = 20, AC = 21, BC = 29
To Find: sin B, cos C and tan B
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Here, θ = B
The side opposite to angle B = AC =21
Hypotenuse = BC =29
So, $\sin B=\frac{A C}{B C}=\frac{21}{29}$
Now, Cos C
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Here, θ = C
Side adjacent to angle C = AC = 21
Hypotenuse = BC = 29
So,$\cos C=\frac{A C}{B C}=\frac{21}{29}$
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Here, θ = B
The side opposite to angle B = AC = 21
The side adjacent to angle B = AB = 20
So, $\tan \mathrm{B}=\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{21}{20}$
To Find: sin B, cos C and tan B
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Here, θ = B
The side opposite to angle B = AC =1
Hypotenuse = BC =√2
So$\sin \mathrm{B}=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{1}{\sqrt{2}}$
Now, Cos C
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Here, θ = C
Side adjacent to angle C = AC = 1
Hypotenuse = BC = √2
So, $\cos C=\frac{A C}{B C}=\frac{1}{\sqrt{2}}$
Now, tan B
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Here, θ = B
The side opposite to angle B = AC = 1
The side adjacent to angle B = AB = 1
So,$\tan B=\frac{A C}{A B}=\frac{1}{1}=1$
Question 5 A
Find the value of the following : (a)
sin θ (b) cos θ (c) tan θ from the figures given below :
Sol :
Firstly, we give the name to the midpoint of BC
i.e. M
BC = BM + MC = 2BM or 2MC
⇒ BM = 5 and MC = 5
Now, we have to
find the value of AM, and we can find out with the help of Pythagoras theorem.
So, In ∆AMB
⇒ (AM)2 +
(BM)2 = (AB)2
⇒ (AM)2 + (5)2 = (13)2
⇒ (AM)2 = (13)2 –
(5)2
Using the identity a2 –b2 = (a+b)
(a – b)
⇒ (AM)2 =
(13–5)(13+5)
⇒ (AM)2 =
(8)(18)
⇒ (AM)2 =
144
⇒ AM =√144
⇒ AM =±12
But side AM can’t be negative. So, AM
= 12
a. sin θ
We know that,
$\sin \theta=\frac{\text {
side opposite to angle } \theta}{\text { hypotenuse }}$
In ∆AMB
Side opposite to θ = AM =
12
Hypotenuse = AB=13
So, $\sin
\theta=\frac{A M}{A B}=\frac{12}{13}$
So, $\sin
\theta=\frac{12}{13}$
b. cos θ
We know that, $\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text {
hypotenuse }}$
In ∆AMB
The side adjacent to θ = BM =
5
Hypotenuse = AB = 13
So, $\cos
\theta=\frac{B M}{A B}=\frac{5}{13}$
So, $\cos \theta=\frac{5}{13}$
c. tan θ
We know that,
$\tan \theta=\frac{\text {
side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
In
∆AMB
Side opposite to θ = AM = 12
The side adjacent
to θ = BM = 5
So, $\tan \theta=\frac{\mathrm{AM}}{\mathrm{BM}}=\frac{12}{5}$
So, $\tan \theta=\frac{12}{5}$
Sol :
Firstly, we give the name to the midpoint of BC i.e. M
BC = BM + MC = 2BM or 2MC
⇒ BM = 5 and MC = 5
Now, we have to find the value of AM, and we can find out with the help of Pythagoras theorem.
So, In ∆AMB
⇒ (AM)2 + (BM)2 = (AB)2
⇒ (AM)2 + (5)2 = (13)2
⇒ (AM)2 = (13)2 – (5)2
Using the identity a2 –b2 = (a+b) (a – b)
⇒ (AM)2 = (13–5)(13+5)
⇒ (AM)2 = (8)(18)
⇒ (AM)2 = 144
⇒ AM =√144
⇒ AM =±12
But side AM can’t be negative. So, AM = 12
a. sin θ
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
In ∆AMB
Side opposite to θ = AM = 12
Hypotenuse = AB=13
So, $\sin \theta=\frac{A M}{A B}=\frac{12}{13}$
So, $\sin \theta=\frac{12}{13}$
b. cos θ
We know that, $\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
In ∆AMB
The side adjacent to θ = BM = 5
Hypotenuse = AB = 13
So, $\cos \theta=\frac{B M}{A B}=\frac{5}{13}$
So, $\cos \theta=\frac{5}{13}$
c. tan θ
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
In ∆AMB
Side opposite to θ = AM = 12
The side adjacent to θ = BM = 5
So, $\tan \theta=\frac{\mathrm{AM}}{\mathrm{BM}}=\frac{12}{5}$
So, $\tan \theta=\frac{12}{5}$
Question 5 B
Find the value of the following : (a)
sin θ (b) cos θ (c) tan θ from the figures given below :
Sol :
Firstly, we have to find the value of XM and we can find out with the help of
Pythagoras theorem
So, In ∆XMZ
⇒ (XM)2 + (MZ)2 = (XZ)2
⇒ (XM)2 + (16)2 = (20)2
⇒ (XM)2 = (20)2 – (16)2
Using the identity a2 –b2 = (a+b) (a –
b)
⇒ (XM)2 =
(20–16)(20+16)
⇒ (XM)2 =
(4)(36)
⇒ (XM)2 =
144
⇒ XM =√144
⇒ XM =±12
But side XM can’t be negative. So, XM = 12
Now, In ∆XMY we have the value of XM and MY but we don’t have the value of
XY.
So, again we apply the Pythagoras theorem in
∆XMY
⇒ (XM)2 +
(MY)2 = (XY)2
⇒ (12)2 +
(5)2 = (XY)2
⇒ 144 + 25 =
(XY)2
⇒ (XY)2 =
169
⇒ XY =√169
⇒ XY =±13
But side XY can’t be negative. So, XY = 13
a. sin θ
We know
that,
$\sin \theta=\frac{\text { side opposite to angle }
\theta}{\text { hypotenuse }}$
In
∆XMY
Side opposite to θ = MY = 5
Hypotenuse = XY = 13
So, $\sin
\theta=\frac{\mathrm{MY}}{\mathrm{XY}}=\frac{5}{13}$
b. cos θ
We know
that,
$\cos \theta=\frac{\text { side adjacent to angle }
\theta}{\text { hypotenuse }}$
In
∆XMY
Side adjacent to θ = XM = 12
Hypotenuse = XY = 13
So,$\cos \theta=\frac{\mathrm{XM}}{\mathrm{XY}}=\frac{12}{13}$
c. tan θ
We know
that,
$\tan \theta=\frac{\text { side opposite to angle }
\theta}{\text { side adjacent to angle } \theta}$
In
∆XMY
The side opposite to θ = MY = 5
Side adjacent to θ = XM = 12
So, $\tan \theta=\frac{\mathrm{MY}}{\mathrm{XM}}=\frac{5}{12}$
Firstly, we have to find the value of XM and we can find out with the help of Pythagoras theorem
So, In ∆XMZ
⇒ (XM)2 + (MZ)2 = (XZ)2
⇒ (XM)2 + (16)2 = (20)2
⇒ (XM)2 = (20)2 – (16)2
Using the identity a2 –b2 = (a+b) (a – b)
⇒ (XM)2 = (20–16)(20+16)
⇒ (XM)2 = (4)(36)
⇒ (XM)2 = 144
⇒ XM =√144
⇒ XM =±12
But side XM can’t be negative. So, XM = 12
Now, In ∆XMY we have the value of XM and MY but we don’t have the value of XY.
So, again we apply the Pythagoras theorem in ∆XMY
⇒ (XM)2 + (MY)2 = (XY)2
⇒ (12)2 + (5)2 = (XY)2
⇒ 144 + 25 = (XY)2
⇒ (XY)2 = 169
⇒ XY =√169
⇒ XY =±13
But side XY can’t be negative. So, XY = 13
a. sin θ
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
In ∆XMY
Side opposite to θ = MY = 5
Hypotenuse = XY = 13
So, $\sin \theta=\frac{\mathrm{MY}}{\mathrm{XY}}=\frac{5}{13}$
b. cos θ
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
In ∆XMY
Side adjacent to θ = XM = 12
Hypotenuse = XY = 13
So,$\cos \theta=\frac{\mathrm{XM}}{\mathrm{XY}}=\frac{12}{13}$
c. tan θ
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
In ∆XMY
The side opposite to θ = MY = 5
Side adjacent to θ = XM = 12
So, $\tan \theta=\frac{\mathrm{MY}}{\mathrm{XM}}=\frac{5}{12}$
Question 6
In ∆PQR, ∠Q is a right angle PQ = 3, QR = 4. If ∠P=α and ∠R=β, then find
the values of(i) sin α (ii) cos α
(iii) tan α (iv) sin
β
(v) cos β (vi) tan β
Sol :
Given : PQ = 3, QR = 4
⇒ (PQ)2 + (QR)2 =
(PR)2
⇒ (3)2 +
(4)2 = (PR)2
⇒ 9 + 16 =
(PR)2
⇒ (PR)2 =
25
⇒ PR =√25
⇒ PR =±5
But side PR can’t be negative. So, PR =
5
(i) sin α
We know
that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Here, θ = α
The side opposite to
angle α = QR =4
Hypotenuse = PR =5
So, $\sin \alpha=\frac{4}{5}$
(ii) cos α
We know that,
$\cos \theta=\frac{\text { side
adjacent to angle } \theta}{\text { hypotenuse }}$
Here, θ
= α
The side adjacent to angle α = PQ =3
Hypotenuse = PR =5
So, $\cos
\alpha=\frac{3}{5}$
(iii) tan α
We know that,
$\tan \theta=\frac{\text { side opposite
to angle } \theta}{\text { side adjacent to angle } \theta}$
Here, θ = α
Side opposite to angle α = QR =4
Side adjacent to angle α = PQ =3
So,$\tan
\alpha=\frac{4}{3}$
(iv) sin β
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text {
hypotenuse }}$
Here, θ = β
The side opposite to angle β = PQ =3
Hypotenuse = PR
=5
So, $\sin \beta=\frac{3}{5}$
(v) cos β
We know
that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Here, θ = β
Side adjacent to angle β
= QR =4
Hypotenuse = PR =5
So, $\cos
\beta=\frac{4}{5}$
(vi) tan β
We know that,
$\tan \theta=\frac{\text { side opposite
to angle } \theta}{\text { side adjacent to angle } \theta}$
Here, θ = β
Side opposite to angle β = PQ =3
Side adjacent to angle β = QR =4
So, $\tan
\beta=\frac{3}{4}$
(iii) tan α (iv) sin β
(v) cos β (vi) tan β
Sol :
⇒ (PQ)2 + (QR)2 = (PR)2
⇒ (3)2 + (4)2 = (PR)2
⇒ 9 + 16 = (PR)2
⇒ (PR)2 = 25
⇒ PR =√25
⇒ PR =±5
But side PR can’t be negative. So, PR = 5
(i) sin α
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Here, θ = α
The side opposite to angle α = QR =4
Hypotenuse = PR =5
So, $\sin \alpha=\frac{4}{5}$
(ii) cos α
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Here, θ = α
The side adjacent to angle α = PQ =3
Hypotenuse = PR =5
So, $\cos \alpha=\frac{3}{5}$
(iii) tan α
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Here, θ = α
Side opposite to angle α = QR =4
Side adjacent to angle α = PQ =3
So,$\tan \alpha=\frac{4}{3}$
(iv) sin β
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Here, θ = β
The side opposite to angle β = PQ =3
Hypotenuse = PR =5
So, $\sin \beta=\frac{3}{5}$
(v) cos β
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Here, θ = β
Side adjacent to angle β = QR =4
Hypotenuse = PR =5
So, $\cos \beta=\frac{4}{5}$
(vi) tan β
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Here, θ = β
Side opposite to angle β = PQ =3
Side adjacent to angle β = QR =4
So, $\tan \beta=\frac{3}{4}$
Question 7 A
If $\sin \theta=\frac{4}{5}$
,then find the values of cos θ and tan θ.Sol :
Given: $\sin \theta=\frac{4}{5}$
We know that,
$\sin \theta=\frac{\text {
side opposite to angle } \theta}{\text { hypotenuse }}$
Or $\sin
\theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$\sin \theta=\frac{4}{5} \Rightarrow
\frac{\mathrm{P}}{\mathrm{H}}=\frac{4}{5} \Rightarrow \frac{\mathrm{AB}}{\mathrm{AC}}=\frac{4}{5}$
Let,
Perpendicular =AB =4k
and
Hypotenuse =AC =5k
where, k is any positive integer
So, by Pythagoras theorem, we can find the third side of a triangle
In right angled ∆ ABC, we
have
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (4k)2 + (BC)2 = (5k)2
⇒ 16k2 + (BC)2 =
25k2
⇒ (BC)2 = 25
k2 –16 k2
⇒ (BC)2 = 9 k2
⇒ BC =√9 k2
⇒ BC =±3k
But side BC can’t be negative. So, BC = 3k
Now, we have to find the value of cos θ and tan θ
We know
that,
$\cos \theta=\frac{\text { base }}{\text { hypotenuse }}$
The side
adjacent to angle θ or base = BC
=3k
Hypotenuse = AC =5k
So, $\cos
\theta=\frac{3 \mathrm{k}}{5 \mathrm{k}}=\frac{3}{5}$
Now,
We know that,$\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
Perpendicular = AB =4k
Base = BC =3k
So, $\tan \theta=\frac{4 k}{3 k}=\frac{4}{3}$
Given: $\sin \theta=\frac{4}{5}$
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Or $\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$\sin \theta=\frac{4}{5} \Rightarrow \frac{\mathrm{P}}{\mathrm{H}}=\frac{4}{5} \Rightarrow \frac{\mathrm{AB}}{\mathrm{AC}}=\frac{4}{5}$
Let,
Perpendicular =AB =4k
and Hypotenuse =AC =5k
where, k is any positive integer
So, by Pythagoras theorem, we can find the third side of a triangle
In right angled ∆ ABC, we have
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (4k)2 + (BC)2 = (5k)2
⇒ 16k2 + (BC)2 = 25k2
⇒ (BC)2 = 25 k2 –16 k2
⇒ (BC)2 = 9 k2
⇒ BC =√9 k2
⇒ BC =±3k
But side BC can’t be negative. So, BC = 3k
Now, we have to find the value of cos θ and tan θ
We know that,
$\cos \theta=\frac{\text { base }}{\text { hypotenuse }}$
The side adjacent to angle θ or base = BC =3k
Hypotenuse = AC =5k
So, $\cos \theta=\frac{3 \mathrm{k}}{5 \mathrm{k}}=\frac{3}{5}$
Now,
We know that,$\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
Perpendicular = AB =4k
Base = BC =3k
So, $\tan \theta=\frac{4 k}{3 k}=\frac{4}{3}$
Question 7 B
If $\sin
\mathrm{A}=\frac{3}{4}$ ,calculate cos A and tan A.Sol :
Given: Sin A $=\frac{3}{4}$
We know that,
$\sin \theta=\frac{\text {
side opposite to angle } \theta}{\text { hypotenuse }}$
Or $\sin
\theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$\sin \theta=\frac{3}{4} \Rightarrow
\frac{\mathrm{P}}{\mathrm{H}}=\frac{3}{4} \Rightarrow \frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3}{4}$
Let,
Side opposite to angle θ = BC
=3k
and Hypotenuse = AC =4k
where, k is any positive integer
So,
by Pythagoras theorem, we can find the third side of a triangle
⇒ (AB)2 + (BC)2 =
(AC)2
⇒ (AB)2 +
(3k)2 = (4k)2
⇒ (AB)2 + 9k2 = 16k2
⇒ (AB)2 = 16 k2 – 9
k2
⇒ (AB)2 = 7
k2
⇒ AB =k√7
So, AB = k√7
Now, we have to find the value of cos A and tan A
We know
that,
$\cos \theta=\frac{\text { Side adjacent to angle } \theta}{\text { hypotenuse }}$
Here, θ = A
The side adjacent to
angle A = AB =k√7
Hypotenuse = AC =4k
So,$\cos
A=\frac{k \sqrt{7}}{4 k}=\frac{\sqrt{7}}{4}$
Now,
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side
adjacent to angle } \theta}$
The side opposite to angle A =
BC =3k
The side adjacent to angle A = AB
=k√7
So,$\tan \mathrm{A}=\frac{3 \mathrm{k}}{\mathrm{k}
\sqrt{7}}=\frac{3}{\sqrt{7}}$
Given: Sin A $=\frac{3}{4}$
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Or $\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$\sin \theta=\frac{3}{4} \Rightarrow \frac{\mathrm{P}}{\mathrm{H}}=\frac{3}{4} \Rightarrow \frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3}{4}$
Let,
Side opposite to angle θ = BC =3k
and Hypotenuse = AC =4k
where, k is any positive integer
So, by Pythagoras theorem, we can find the third side of a triangle
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (AB)2 + (3k)2 = (4k)2
⇒ (AB)2 + 9k2 = 16k2
⇒ (AB)2 = 16 k2 – 9 k2
⇒ (AB)2 = 7 k2
⇒ AB =k√7
So, AB = k√7
Now, we have to find the value of cos A and tan A
We know that,
$\cos \theta=\frac{\text { Side adjacent to angle } \theta}{\text { hypotenuse }}$
Here, θ = A
The side adjacent to angle A = AB =k√7
Hypotenuse = AC =4k
So,$\cos A=\frac{k \sqrt{7}}{4 k}=\frac{\sqrt{7}}{4}$
Now,
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
The side opposite to angle A = BC =3k
The side adjacent to angle A = AB =k√7
So,$\tan \mathrm{A}=\frac{3 \mathrm{k}}{\mathrm{k} \sqrt{7}}=\frac{3}{\sqrt{7}}$
Question 8
If $\sin \theta=\frac{3}{5}$
, then find the values cos θ and tan θ.
Sol :
Given:$\sin \theta=\frac{3}{5}$
We know that,
$\sin \theta=\frac{\text {
side opposite to angle } \theta}{\text { hypotenuse }}$
Or $\sin
\theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$\sin \theta=\frac{3}{5} \Rightarrow
\frac{\mathrm{P}}{\mathrm{H}}=\frac{3}{5} \Rightarrow \frac{\mathrm{AB}}{\mathrm{AC}}=\frac{3}{5}$
Let,
Perpendicular =AB =3k
and
Hypotenuse =AC =5k
where, k is any positive integer
So, by Pythagoras theorem, we can find the third side of a triangle
⇒ (AB)2 + (BC)2 =
(AC)2
⇒ (3k)2 +
(BC)2 = (5k)2
⇒ 9k2 + (BC)2 = 25k2
⇒ (BC)2 = 25 k2 – 9
k2
⇒ (BC)2 = 16
k2
⇒ BC =√16 k2
⇒ BC =±4k
But side
BC can’t be negative. So, BC = 4k
Now, we have to find the value of cos θ and tan
θ
We know that,
$\cos \theta=\frac{\text { side adjacent to angle }
\theta}{\text { hypotenuse }}$
The side adjacent to angle θ = BC =4k
Hypotenuse = AC
=5k
So, $\cos \theta=\frac{4 \mathrm{k}}{5
\mathrm{k}}=\frac{4}{5}$
Now, tan θ
We know
that,
$\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
Perpendicular = AB =3k
Base = BC =4k
So, $\tan \theta=\frac{3 \mathrm{k}}{4 \mathrm{k}}=\frac{3}{4}$
Given:$\sin \theta=\frac{3}{5}$
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Or $\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$\sin \theta=\frac{3}{5} \Rightarrow \frac{\mathrm{P}}{\mathrm{H}}=\frac{3}{5} \Rightarrow \frac{\mathrm{AB}}{\mathrm{AC}}=\frac{3}{5}$
Let,
Perpendicular =AB =3k
and Hypotenuse =AC =5k
where, k is any positive integer
So, by Pythagoras theorem, we can find the third side of a triangle
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (3k)2 + (BC)2 = (5k)2
⇒ 9k2 + (BC)2 = 25k2
⇒ (BC)2 = 25 k2 – 9 k2
⇒ (BC)2 = 16 k2
⇒ BC =√16 k2
⇒ BC =±4k
But side BC can’t be negative. So, BC = 4k
Now, we have to find the value of cos θ and tan θ
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
The side adjacent to angle θ = BC =4k
Hypotenuse = AC =5k
So, $\cos \theta=\frac{4 \mathrm{k}}{5 \mathrm{k}}=\frac{4}{5}$
Now, tan θ
We know that,
$\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
Perpendicular = AB =3k
Base = BC =4k
So, $\tan \theta=\frac{3 \mathrm{k}}{4 \mathrm{k}}=\frac{3}{4}$
Question 9
If $\cos \theta=\frac{4}{5}$
, then find the value of tan θ.Sol :
We know that,
$\cos \theta=\frac{\text {
side adjacent to angle } \theta}{\text { hypotenuse }}$
Or $\cos
\theta=\frac{\text { base }}{\text { Hypotenuse }}$
$\cos \theta=\frac{4}{5} \Rightarrow
\frac{B}{H}=\frac{4}{5} \Rightarrow \frac{B C}{A C}=\frac{4}{5}$
Let,
Base =BC = 4k
Hypotenuse =AC = 5k
Where, k ia any positive integer
So, by Pythagoras theorem, we can
find the third side of a triangle
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (AB)2 + (4k)2 =
(5k)2
⇒ (AB)2 +
16k2 = 25k2
⇒ (AB)2 = 25 k2 –16 k2
⇒ (AB)2 = 9 k2
⇒ AB =√9
k2
⇒ AB =±3k
But side AB can’t be negative. So, AB
= 3k
Now, we have to find tan θ
We know
that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle }
\theta}$
Side opposite to angle θ = BC =4k
Side adjacent to angle θ = AB
=3k
So,$\tan \theta=\frac{4 k}{3
k}=\frac{4}{3}$
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Or $\cos \theta=\frac{\text { base }}{\text { Hypotenuse }}$
$\cos \theta=\frac{4}{5} \Rightarrow \frac{B}{H}=\frac{4}{5} \Rightarrow \frac{B C}{A C}=\frac{4}{5}$
Let,
Base =BC = 4k
Hypotenuse =AC = 5k
Where, k ia any positive integer
So, by Pythagoras theorem, we can find the third side of a triangle
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (AB)2 + (4k)2 = (5k)2
⇒ (AB)2 + 16k2 = 25k2
⇒ (AB)2 = 25 k2 –16 k2
⇒ (AB)2 = 9 k2
⇒ AB =√9 k2
⇒ AB =±3k
But side AB can’t be negative. So, AB = 3k
Now, we have to find tan θ
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Side opposite to angle θ = BC =4k
Side adjacent to angle θ = AB =3k
So,$\tan \theta=\frac{4 k}{3 k}=\frac{4}{3}$
Question 10 A
If $\tan
\theta=\frac{3}{4}$ then find the values of cos θ and sin
θ.
Sol :
We know that,
$\tan \theta=\frac{\text {
side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
$\tan
\theta=\frac{3}{4}$
$\Rightarrow \frac{P}{B}=\frac{3}{4}$
$\Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{3}{4}$
Let,
The side opposite to
angle θ =AB = 3k
The side adjacent to angle θ =BC = 4k
where k is any positive integer
Firstly we have to find the value of
AC.
So, we can find the value of AC with the help of Pythagoras
theorem
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (3k)2 + (4k)2 = (AC)2
⇒ (AC)2 = 9 k2+16
k2
⇒ (AC)2 = 25
k2
⇒ AC =√25 k2
⇒ AC =±5k
But side
AC can’t be negative. So, AC = 5k
Now, we will find the sin θ and cos
θ
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle θ = AB = 3k
and Hypotenuse = AC = 5k
So, $\sin \theta=\frac{A B}{A
C}=\frac{3 k}{5 k}=\frac{3}{5}$
Now, We know that
$\cos \theta=\frac{\text {
side adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to
angle θ = BC = 4k
and Hypotenuse = AC =
5k
So,$\cos \theta=\frac{B C}{A C}=\frac{4 k}{5 k}=\frac{4}{5}$
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
$\tan \theta=\frac{3}{4}$
Let,
The side opposite to angle θ =AB = 3k
The side adjacent to angle θ =BC = 4k
where k is any positive integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (3k)2 + (4k)2 = (AC)2
⇒ (AC)2 = 9 k2+16 k2
⇒ (AC)2 = 25 k2
⇒ AC =√25 k2
⇒ AC =±5k
But side AC can’t be negative. So, AC = 5k
Now, we will find the sin θ and cos θ
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle θ = AB = 3k
and Hypotenuse = AC = 5k
So, $\sin \theta=\frac{A B}{A C}=\frac{3 k}{5 k}=\frac{3}{5}$
Now, We know that
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to angle θ = BC = 4k
and Hypotenuse = AC = 5k
So,$\cos \theta=\frac{B C}{A C}=\frac{4 k}{5 k}=\frac{4}{5}$
Question 10 B
If tan A= 4/3. Find
the other trigonometric ratios of the angle A.Sol :
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent
to angle } \theta}$
Or $\tan \theta=\frac{\text { perpendicular
}}{\text { base }}$
Here, θ = A
$\tan \mathrm{A}=\frac{4}{3}$
$\Rightarrow \frac{P}{B}=\frac{4}{3}$
$\Rightarrow \frac{\mathrm{BC}}{\mathrm{AB}}=\frac{4}{3}$
Let,
The side opposite to
angle A =BC = 4k
The side adjacent to angle A =AB = 3k
where k is any positive integer
Firstly we have to find the value of
AC.
So, we can find the value of AC with the help of Pythagoras
theorem
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (3k)2 + (4k)2 = (AC)2
⇒ (AC)2 = 9 k2 +16
k2
⇒ (AC)2 = 25
k2
⇒ AC =√25 k2
⇒ AC =±5k
But side
AC can’t be negative. So, AC = 5k
Now, we will find the sin A and cos
A
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle A = BC = 4k
and Hypotenuse = AC = 5k
So, $\sin A=\frac{B C}{A
C}=\frac{4 k}{5 k}=\frac{4}{5}$
Now, We know that
$\cos \theta=\frac{\text { side
adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to
angle A = AB = 3k
and Hypotenuse = AC =
5k
So, $\cos A=\frac{A B}{A C}=\frac{3 k}{5
k}=\frac{3}{5}$
Now, we find other trigonometric ratios
$\operatorname{cosec}
\mathrm{A}=\frac{1}{\sin \mathrm{A}}$
$=\frac{1}{\frac{4}{5}}$
$=\frac{5}{4}$
$\sec \mathrm{A}=\frac{1}{\cos
\mathrm{A}}$
$=\frac{1}{\frac{3}{5}}$
$=\frac{5}{3}$
$\cot A=\frac{1}{\tan
A}$
$=\frac{1}{\frac{4}{3}}$
$=\frac{3}{4}$
Let,
The side opposite to angle A =BC = 4k
The side adjacent to angle A =AB = 3k
where k is any positive integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (3k)2 + (4k)2 = (AC)2
⇒ (AC)2 = 9 k2 +16 k2
⇒ (AC)2 = 25 k2
⇒ AC =√25 k2
⇒ AC =±5k
But side AC can’t be negative. So, AC = 5k
Now, we will find the sin A and cos A
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle A = BC = 4k
and Hypotenuse = AC = 5k
So, $\sin A=\frac{B C}{A C}=\frac{4 k}{5 k}=\frac{4}{5}$
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to angle A = AB = 3k
and Hypotenuse = AC = 5k
Now, we find other trigonometric ratios
$\operatorname{cosec} \mathrm{A}=\frac{1}{\sin \mathrm{A}}$
$=\frac{1}{\frac{4}{5}}$
$=\frac{5}{4}$
$\sec \mathrm{A}=\frac{1}{\cos \mathrm{A}}$
$=\frac{1}{\frac{3}{5}}$
$=\frac{5}{3}$
$\cot A=\frac{1}{\tan A}$
$=\frac{1}{\frac{4}{3}}$
$=\frac{3}{4}$
Question 11
If cot $\theta=\frac{12}{5}$, then find the value of sin θ.Sol :
We know that,
$\cot \theta=\frac{\text { side adjacent
to angle } \theta}{\text { side opposite to angle } \theta}$
Or $\cot
\theta=\frac{\text { base }}{\text { perpendicular }}$
$\cot \theta=\frac{12}{5} \Rightarrow
\frac{\mathrm{B}}{\mathrm{P}}=\frac{12}{5} \Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{12}{5}$
Let,
Side adjacent to angle θ =AB = 12k
The
side opposite to angle θ =BC = 5k
where k is any positive
integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 =
(AC)2
⇒ (12k)2 +
(5k)2 = (AC)2
⇒ (AC)2 = 144 k2 +25 k2
⇒ (AC)2 = 169 k2
⇒ AC =√169
k2
⇒ AC =±13k
But side AC can’t be negative. So, AC
= 13k
Now, we will find the sin θ
$\sin \theta=\frac{\text { side
opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to
angle θ = BC = 5k
and Hypotenuse = AC =
13k
So, $\sin \theta=\frac{B C}{A C}=\frac{5 k}{13
k}=\frac{5}{13}$
$\cot \theta=\frac{\text { side adjacent to angle } \theta}{\text { side opposite to angle } \theta}$
Or $\cot \theta=\frac{\text { base }}{\text { perpendicular }}$
$\cot \theta=\frac{12}{5} \Rightarrow \frac{\mathrm{B}}{\mathrm{P}}=\frac{12}{5} \Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{12}{5}$
Let,
Side adjacent to angle θ =AB = 12k
The side opposite to angle θ =BC = 5k
where k is any positive integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (12k)2 + (5k)2 = (AC)2
⇒ (AC)2 = 144 k2 +25 k2
⇒ (AC)2 = 169 k2
⇒ AC =√169 k2
⇒ AC =±13k
But side AC can’t be negative. So, AC = 13k
Now, we will find the sin θ
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle θ = BC = 5k
and Hypotenuse = AC = 13k
So, $\sin \theta=\frac{B C}{A C}=\frac{5 k}{13 k}=\frac{5}{13}$
Question 12
If tan $\theta=\frac{5}{12}$, then find the value of cos θ.Sol :
We know that,
$\tan \theta=\frac{\text { side opposite
to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan
\theta=\frac{\text { perpendicular }}{\text { base }}$
$\tan \theta=\frac{5}{12} \Rightarrow
\frac{\mathrm{P}}{\mathrm{B}}=\frac{5}{12} \Rightarrow \frac{\mathrm{BC}}{\mathrm{AB}}=\frac{5}{12}$
Let,
The side opposite to
angle θ =BC = 5k
The side adjacent to angle θ =AB = 12k
where k is any positive integer
Firstly we have to find the value of
AC.
So, we can find the value of AC with the help of Pythagoras
theorem
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (12k)2 + (5k)2 = (AC)2
⇒ (AC)2 = 144 k2 +25
k2
⇒ (AC)2 = 169
k2
⇒ AC =√169 k2
⇒ AC =±13k
But
side AC can’t be negative. So, AC = 13k
Now, We know that
$\cos
\theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent
to angle θ = AB = 12k
and Hypotenuse = AC =
13k
So, $\cos \theta=\frac{A B}{A C}=\frac{12 k}{13
k}=\frac{12}{13}$
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
$\tan \theta=\frac{5}{12} \Rightarrow \frac{\mathrm{P}}{\mathrm{B}}=\frac{5}{12} \Rightarrow \frac{\mathrm{BC}}{\mathrm{AB}}=\frac{5}{12}$
Let,
The side opposite to angle θ =BC = 5k
The side adjacent to angle θ =AB = 12k
where k is any positive integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (12k)2 + (5k)2 = (AC)2
⇒ (AC)2 = 144 k2 +25 k2
⇒ (AC)2 = 169 k2
⇒ AC =√169 k2
⇒ AC =±13k
But side AC can’t be negative. So, AC = 13k
Now, We know that
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to angle θ = AB = 12k
and Hypotenuse = AC = 13k
So, $\cos \theta=\frac{A B}{A C}=\frac{12 k}{13 k}=\frac{12}{13}$
Question 13
If sin $\theta=\frac{12}{13}$, then find the value of cos θ and tan θ.
Sol :
Given: $\sin \theta=\frac{12}{13}$
We know that,
$\sin \theta=\frac{\text { side opposite
to angle } \theta}{\text { hypotenuse }}$
Or $\sin \theta=\frac{\text {
Perpendicular }}{\text { Hypotenuse }}$
$\sin \theta=\frac{12}{13} \Rightarrow
\frac{\mathrm{P}}{\mathrm{H}}=\frac{12}{13} \Rightarrow \frac{\mathrm{AB}}{\mathrm{AC}}=\frac{12}{13}$
Let,
Side opposite to angle θ =
12k
and Hypotenuse = 13k
where, k is any positive
integer
So, by Pythagoras theorem, we can find the third side of a
triangle
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (12k)2 + (BCk)2 = (13)2
⇒ 144 k2 + (BC)2 = 169
k2
⇒ (BC)2 = 169
k2 –144 k2
⇒ (BC)2 = 25 k2
⇒ BC =√25 k2
⇒ BC =±5k
But side BC can’t be negative. So, BC = 5k
Now, we have to find the value of cos θ and tan θ
We know
that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to angle θ = BC
=5k
Hypotenuse = AC =13k
So, $\cos
\theta=\frac{5 \mathrm{k}}{13 \mathrm{k}}=\frac{5}{13}$
Now, tan θ
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side
adjacent to angle } \theta}$
side opposite to angle θ = AB
=12k
Side adjacent to angle θ = BC =5k
So, $\tan \theta=\frac{12 \mathrm{k}}{5
\mathrm{k}}=\frac{12}{5}$
Given: $\sin \theta=\frac{12}{13}$
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Or $\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$\sin \theta=\frac{12}{13} \Rightarrow \frac{\mathrm{P}}{\mathrm{H}}=\frac{12}{13} \Rightarrow \frac{\mathrm{AB}}{\mathrm{AC}}=\frac{12}{13}$
Let,
Side opposite to angle θ = 12k
and Hypotenuse = 13k
where, k is any positive integer
So, by Pythagoras theorem, we can find the third side of a triangle
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (12k)2 + (BCk)2 = (13)2
⇒ 144 k2 + (BC)2 = 169 k2
⇒ (BC)2 = 169 k2 –144 k2
⇒ (BC)2 = 25 k2
⇒ BC =√25 k2
⇒ BC =±5k
But side BC can’t be negative. So, BC = 5k
Now, we have to find the value of cos θ and tan θ
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to angle θ = BC =5k
Hypotenuse = AC =13k
So, $\cos \theta=\frac{5 \mathrm{k}}{13 \mathrm{k}}=\frac{5}{13}$
Now, tan θ
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
side opposite to angle θ = AB =12k
Side adjacent to angle θ = BC =5k
So, $\tan \theta=\frac{12 \mathrm{k}}{5 \mathrm{k}}=\frac{12}{5}$
Question 14
If tan θ =0.75, then find the value of sin
θ.
Sol :
We know that,
$\tan \theta=\frac{\text { side opposite
to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan
\theta=\frac{\text { perpendicular }}{\text { base }}$
Given: tan θ
=0.75
$\Rightarrow \tan \theta=\frac{75}{100}=\frac{3}{4}$
$\tan \theta=\frac{3}{4} \Rightarrow
\frac{\mathrm{P}}{\mathrm{B}}=\frac{3}{4} \Rightarrow \frac{\mathrm{BC}}{\mathrm{AB}}=\frac{3}{4}$
Let,
The side opposite to
angle θ =BC = 3k
The side adjacent to angle θ =AB = 4k
Firstly we have to find
the value of AC.
So, we can find the value of AC with the help of Pythagoras
theorem
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (4k)2 + (3k)2 = (AC)2
⇒ (AC)2 = 16 k2 +9
k2
⇒ (AC)2 = 25
k2
⇒ AC =√25
k2
⇒ AC =±5k
But side AC can’t be negative. So, AC
= 5k
Now, we will find the sin θ
$\sin \theta=\frac{\text { side
opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to
angle θ = BC = 3k
and Hypotenuse = AC =
5k
So, $\sin \theta=\frac{B C}{A C}=\frac{3 k}{5
k}=\frac{3}{5}$
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
Given: tan θ =0.75
$\Rightarrow \tan \theta=\frac{75}{100}=\frac{3}{4}$
$\tan \theta=\frac{3}{4} \Rightarrow \frac{\mathrm{P}}{\mathrm{B}}=\frac{3}{4} \Rightarrow \frac{\mathrm{BC}}{\mathrm{AB}}=\frac{3}{4}$
Let,
The side opposite to angle θ =BC = 3k
The side adjacent to angle θ =AB = 4k
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (4k)2 + (3k)2 = (AC)2
⇒ (AC)2 = 16 k2 +9 k2
⇒ (AC)2 = 25 k2
⇒ AC =√25 k2
⇒ AC =±5k
But side AC can’t be negative. So, AC = 5k
Now, we will find the sin θ
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle θ = BC = 3k
and Hypotenuse = AC = 5k
So, $\sin \theta=\frac{B C}{A C}=\frac{3 k}{5 k}=\frac{3}{5}$
Question 15
If tan B= √3, then find the values of sin B
and cos B.
Sol :
We know that,
$\tan
\theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
Given: tan B = √3
$\Rightarrow \tan \mathrm{B}=\frac{\sqrt{3}}{1}$
$\tan
\mathrm{B}=\frac{\sqrt{3}}{1} \Rightarrow \frac{\mathrm{P}}{\mathrm{B}}=\frac{\sqrt{3}}{1} \Rightarrow
\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\sqrt{3}}{1}$
Let,
Side opposite to angle B =AC =
√3k
The side adjacent to
angle B =AB = 1k
where k is any positive integer
Firstly we have to find the value of BC.
So, we can find the
value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (AC)2 = (BC)2
⇒ (1k)2 + (√3k)2 = (BC)2
⇒ (BC)2 = 1 k2 +3
k2
⇒ (BC)2 = 4
k2
⇒ BC =√2 k2
⇒ BC =±2k
But
side BC can’t be negative. So, BC = 2k
Now, we will find the sin B and cos
B
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle B = AC = k√3
and Hypotenuse = BC = 2k
So, $\sin \mathrm{B}=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{k} \sqrt{3}}{2
\mathrm{k}}=\frac{\sqrt{3}}{2}$
Now, we know that,
$\cos
\theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
The side
adjacent to angle B = AB =1k
Hypotenuse = BC =2k
So, $\cos
\mathrm{B}=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{1 \mathrm{k}}{2 \mathrm{k}}=\frac{1}{2}$
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
Given: tan B = √3
$\Rightarrow \tan \mathrm{B}=\frac{\sqrt{3}}{1}$
$\tan \mathrm{B}=\frac{\sqrt{3}}{1} \Rightarrow \frac{\mathrm{P}}{\mathrm{B}}=\frac{\sqrt{3}}{1} \Rightarrow \frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\sqrt{3}}{1}$
Let,
Side opposite to angle B =AC = √3k
The side adjacent to angle B =AB = 1k
where k is any positive integer
Firstly we have to find the value of BC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (AC)2 = (BC)2
⇒ (1k)2 + (√3k)2 = (BC)2
⇒ (BC)2 = 1 k2 +3 k2
⇒ (BC)2 = 4 k2
⇒ BC =√2 k2
⇒ BC =±2k
But side BC can’t be negative. So, BC = 2k
Now, we will find the sin B and cos B
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle B = AC = k√3
and Hypotenuse = BC = 2k
So, $\sin \mathrm{B}=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{k} \sqrt{3}}{2 \mathrm{k}}=\frac{\sqrt{3}}{2}$
Now, we know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
The side adjacent to angle B = AB =1k
Hypotenuse = BC =2k
So, $\cos \mathrm{B}=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{1 \mathrm{k}}{2 \mathrm{k}}=\frac{1}{2}$
Question 16
If $\tan
\theta=\frac{\mathrm{m}}{\mathrm{n}}$, then find the values of cos θ and sin θ.
Sol :
We know that,
$\tan \theta=\frac{\text { side opposite
to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan
\theta=\frac{\text { perpendicular }}{\text { base }}$
Here, $\tan
\theta=\frac{\mathrm{m}}{\mathrm{n}}$
So, Side opposite to angle θ =AC = m
The side adjacent to angle θ =AB =
n
Firstly we have to find the value of BC.
So, we
can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (AC)2 = (BC)2
⇒ (n)2 + (m)2 = (BC)2
⇒ (BC)2 = m2 + n2
⇒ BC =√ m2 + n2
So, BC =√(m2 +
n2)
Now, we will find the sin B and cos B
$\sin
\theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite
to angle θ = AC = m
and Hypotenuse = BC =√(m2 + n2)
So, $\sin \theta=\frac{A C}{B C}=\frac{m}{\sqrt{m^{2}+n^{2}}}$
Now, we know that,
$\cos \theta=\frac{\text { side
adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to
angle θ = AB =n
Hypotenuse = BC =√(m2 +
n2)
So, $\cos \theta=\frac{A B}{B
C}=\frac{n}{\sqrt{m^{2}+n^{2}}}$
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
Here, $\tan \theta=\frac{\mathrm{m}}{\mathrm{n}}$
So, Side opposite to angle θ =AC = m
The side adjacent to angle θ =AB = n
Firstly we have to find the value of BC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (AC)2 = (BC)2
⇒ (n)2 + (m)2 = (BC)2
⇒ (BC)2 = m2 + n2
⇒ BC =√ m2 + n2
So, BC =√(m2 + n2)
Now, we will find the sin B and cos B
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle θ = AC = m
and Hypotenuse = BC =√(m2 + n2)
So, $\sin \theta=\frac{A C}{B C}=\frac{m}{\sqrt{m^{2}+n^{2}}}$
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to angle θ = AB =n
Hypotenuse = BC =√(m2 + n2)
So, $\cos \theta=\frac{A B}{B C}=\frac{n}{\sqrt{m^{2}+n^{2}}}$
Question 17
If sin θ = √3 cos θ, then find the values of
cos θ and sin θ.
Sol :
Given : sin θ =√3cos θ
$\Rightarrow \frac{\sin \theta}{\cos
\theta}=\sqrt{3}$
⇒ tan θ =√3
We know that,
$\tan \theta=\frac{\text { side opposite
to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan
\theta=\frac{\text { perpendicular }}{\text { base }}$
and tan θ = √3
$\Rightarrow \tan
\theta=\frac{\sqrt{3}}{1}$
$\tan \theta=\frac{\sqrt{3}}{1} \Rightarrow
\frac{\mathrm{P}}{\mathrm{B}}=\frac{\sqrt{3}}{1} \Rightarrow
\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\sqrt{3}}{1}$
Let,
The side opposite to angle θ =AC = k√3
The
side adjacent to angle θ =AB = 1k
where k is any positive
integer
Firstly we have to find the value of BC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (AC)2 =
(BC)2
⇒ (1k)2 +
(k√3)2 = (BC)2
⇒ (BC)2 = 1 k2 +3
k2
⇒ (BC)2 = 4
k2
⇒ BC =√2 k2
⇒ BC =±2k
But side
BC can’t be negative. So, BC = 2k
Now, we will find the sin θ and cos θ
$\sin
\theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite
to angle θ = AC = k√3
and Hypotenuse = BC = 2k
So,$\sin
\theta=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{k} \sqrt{3}}{2
\mathrm{k}}=\frac{\sqrt{3}}{2}$
Now, we know that,
$\cos
\theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
The side
adjacent to angle θ = AB =1k
Hypotenuse = BC =2k
So, $\cos \theta=\frac{A B}{B
C}=\frac{1 k}{2 k}=\frac{1}{2}$
Given : sin θ =√3cos θ
$\Rightarrow \frac{\sin \theta}{\cos \theta}=\sqrt{3}$
⇒ tan θ =√3
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
and tan θ = √3
$\Rightarrow \tan \theta=\frac{\sqrt{3}}{1}$
$\tan \theta=\frac{\sqrt{3}}{1} \Rightarrow \frac{\mathrm{P}}{\mathrm{B}}=\frac{\sqrt{3}}{1} \Rightarrow \frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\sqrt{3}}{1}$
Let,
The side opposite to angle θ =AC = k√3
The side adjacent to angle θ =AB = 1k
where k is any positive integer
Firstly we have to find the value of BC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (AC)2 = (BC)2
⇒ (1k)2 + (k√3)2 = (BC)2
⇒ (BC)2 = 1 k2 +3 k2
⇒ (BC)2 = 4 k2
⇒ BC =√2 k2
⇒ BC =±2k
But side BC can’t be negative. So, BC = 2k
Now, we will find the sin θ and cos θ
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle θ = AC = k√3
and Hypotenuse = BC = 2k
So,$\sin \theta=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{k} \sqrt{3}}{2 \mathrm{k}}=\frac{\sqrt{3}}{2}$
Now, we know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
The side adjacent to angle θ = AB =1k
Hypotenuse = BC =2k
So, $\cos \theta=\frac{A B}{B C}=\frac{1 k}{2 k}=\frac{1}{2}$
Question 18 A
If $\cot
\theta=\frac{21}{20}$, then find the values of cos θ and sin θ.
Sol :
We know that,
$\cot \theta=\frac{\text { side adjacent
to angle } \theta}{\text { side opposite to angle } \theta}$
Or $\cot
\theta=\frac{\text { base }}{\text { perpendicular }}$
$\cot \theta=\frac{21}{20} \Rightarrow
\frac{\mathrm{B}}{\mathrm{P}}=\frac{21}{20} \Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{21}{20}$
Let,
Side adjacent to angle θ =AB = 21k
The
side opposite to angle θ =BC = 20k
where k is any positive
integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 =
(AC)2
⇒ (21k)2 +
(20k)2 = (AC)2
⇒ (AC)2 = 441 k2 +400 k2
⇒ (AC)2 = 841 k2
⇒ AC =√841 k2
⇒ AC =±29k
But side AC can’t be negative. So, AC = 29k
Now, we will find the sin θ
$\sin \theta=\frac{\text { side opposite to angle }
\theta}{\text { hypotenuse }}$
Side opposite to angle θ =
BC = 20k
and Hypotenuse = AC = 29k
So, $\sin \theta=\frac{B C}{A C}=\frac{20 k}{29 k}=\frac{20}{29}$
Now, we know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text {
hypotenuse }}$
Side adjacent to angle θ = AB =21k
Hypotenuse = AC =29k
So, $\cos \theta=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{21 \mathrm{k}}{29
\mathrm{k}}=\frac{21}{29}$
$\cot \theta=\frac{\text { side adjacent to angle } \theta}{\text { side opposite to angle } \theta}$
Or $\cot \theta=\frac{\text { base }}{\text { perpendicular }}$
$\cot \theta=\frac{21}{20} \Rightarrow \frac{\mathrm{B}}{\mathrm{P}}=\frac{21}{20} \Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{21}{20}$
Let,
Side adjacent to angle θ =AB = 21k
The side opposite to angle θ =BC = 20k
where k is any positive integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (21k)2 + (20k)2 = (AC)2
⇒ (AC)2 = 441 k2 +400 k2
⇒ (AC)2 = 841 k2
⇒ AC =√841 k2
⇒ AC =±29k
But side AC can’t be negative. So, AC = 29k
Now, we will find the sin θ
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle θ = BC = 20k
and Hypotenuse = AC = 29k
So, $\sin \theta=\frac{B C}{A C}=\frac{20 k}{29 k}=\frac{20}{29}$
Now, we know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to angle θ = AB =21k
Hypotenuse = AC =29k
So, $\cos \theta=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{21 \mathrm{k}}{29 \mathrm{k}}=\frac{21}{29}$
Question 18 B
If 15 cot A=18, find sin A and sec A.
Sol :
Given: 15 cot A = 8
$\Rightarrow \cot A=\frac{8}{15}$
And we know that,
$\cot \theta=\frac{\text { side
adjacent to angle } \theta}{\text { side opposite to angle } \theta}$
Or $\cot
\theta=\frac{\text { base }}{\text { perpendicular }}$
$\cot \mathrm{A}=\frac{8}{15} \Rightarrow
\frac{\mathrm{B}}{\mathrm{P}}=\frac{8}{15} \Rightarrow \frac{\mathrm{BC}}{\mathrm{AC}}=\frac{8}{15}$
Let,
Side adjacent to angle A =AB = 8k
The side opposite to angle A =BC =
15k
where k is any positive
integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 =
(AC)2
⇒ (8k)2 +
(15k)2 = (AC)2
⇒ (AC)2 = 64 k2 +225 k2
⇒ (AC)2 = 289 k2
⇒ AC =√289
k2
⇒ AC =±17k
But side AC can’t be negative. So, AC
= 17k
Now, we will find the sin θ
$\sin \theta=\frac{\text { side
opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to
angle θ = BC = 15k
and Hypotenuse = AC =
17k
So, $\sin \theta=\frac{B C}{A C}=\frac{15 k}{17
k}=\frac{15}{17}$
Now, we know that,
$\cos \theta=\frac{\text { side adjacent
to angle } \theta}{\text { hypotenuse }}$
The side adjacent to angle θ = AB =8
Hypotenuse = AC
=17
So, $\cos \theta=\frac{A B}{A C}=\frac{8 k}{17
k}=\frac{8}{17}$
$\therefore \sec \theta=\frac{1}{\cos \theta}$
$=\frac{1}{\frac{8}{17}}$
$=\frac{17}{8}$
Given: 15 cot A = 8
$\Rightarrow \cot A=\frac{8}{15}$
$\cot \theta=\frac{\text { side adjacent to angle } \theta}{\text { side opposite to angle } \theta}$
Or $\cot \theta=\frac{\text { base }}{\text { perpendicular }}$
$\cot \mathrm{A}=\frac{8}{15} \Rightarrow \frac{\mathrm{B}}{\mathrm{P}}=\frac{8}{15} \Rightarrow \frac{\mathrm{BC}}{\mathrm{AC}}=\frac{8}{15}$
Let,
Side adjacent to angle A =AB = 8k
The side opposite to angle A =BC = 15k
where k is any positive integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (8k)2 + (15k)2 = (AC)2
⇒ (AC)2 = 64 k2 +225 k2
⇒ (AC)2 = 289 k2
⇒ AC =√289 k2
⇒ AC =±17k
But side AC can’t be negative. So, AC = 17k
Now, we will find the sin θ
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle θ = BC = 15k
and Hypotenuse = AC = 17k
So, $\sin \theta=\frac{B C}{A C}=\frac{15 k}{17 k}=\frac{15}{17}$
Now, we know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
The side adjacent to angle θ = AB =8
Hypotenuse = AC =17
So, $\cos \theta=\frac{A B}{A C}=\frac{8 k}{17 k}=\frac{8}{17}$
$\therefore \sec \theta=\frac{1}{\cos \theta}$
Question 19
If sin θ = cos θ and 0° < θ <90°, then
find the values of sin θ and cos θ.Sol :
Given: sinθ = cosθ
$\Rightarrow \frac{\sin
\theta}{\cos \theta}=1$
⇒ tan θ = 1
$\tan \theta=\frac{1}{1} \Rightarrow \frac{P}{B}=\frac{1}{1} \Rightarrow \frac{A B}{B
C}=\frac{1}{1}$
Let,
Side opposite to angle θ = AB
=1k
The side adjacent to angle θ = BC
=1k
where k is any positive
integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 =
(AC)2
⇒ (1k)2 +
(1k)2 = (AC)2
⇒ (AC)2 = 1k2 +1k2
⇒ (AC)2 = 2k2
⇒ AC =√2k2
⇒ AC =k√2
So, AC = k√2
Now, we will find the sin θ
$\sin \theta=\frac{\text { side opposite to angle }
\theta}{\text { hypotenuse }}$
Side opposite to angle θ =
AB= 1k
and Hypotenuse = AC = k√2
So, $\sin \theta=\frac{A B}{A C}=\frac{1 k}{k \sqrt{2}}=\frac{1}{\sqrt{2}}$
Now, we know that,
$\cos \theta=\frac{\text { side
adjacent to angle } \theta}{\text { hypotenuse }}$
The side adjacent to
angle θ = BC =1k
Hypotenuse = AC =k√2
So, $\cos
\theta=\frac{B C}{A C}=\frac{1 k}{k \sqrt{2}}=\frac{1}{\sqrt{2}}$
Given: sinθ = cosθ
$\Rightarrow \frac{\sin \theta}{\cos \theta}=1$
⇒ tan θ = 1
Let,
Side opposite to angle θ = AB =1k
The side adjacent to angle θ = BC =1k
where k is any positive integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (1k)2 + (1k)2 = (AC)2
⇒ (AC)2 = 1k2 +1k2
⇒ (AC)2 = 2k2
⇒ AC =√2k2
⇒ AC =k√2
So, AC = k√2
Now, we will find the sin θ
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle θ = AB= 1k
and Hypotenuse = AC = k√2
So, $\sin \theta=\frac{A B}{A C}=\frac{1 k}{k \sqrt{2}}=\frac{1}{\sqrt{2}}$
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
The side adjacent to angle θ = BC =1k
Hypotenuse = AC =k√2
So, $\cos \theta=\frac{B C}{A C}=\frac{1 k}{k \sqrt{2}}=\frac{1}{\sqrt{2}}$
Question 20
If $\sin
\theta=\frac{x^{2}-y^{2}}{x^{2}+y^{2}}$, then find the values of cos θ and $\frac{1}{\tan
\theta}$.
Sol :
$\sin \theta=\frac{x^{2}-y^{2}}{x^{2}+v^{2}}$
We know that,
$\sin \theta=\frac{\text { side opposite
to angle } \theta}{\text { hypotenuse }}$
Or, $\sin \theta=\frac{\text {
Perpendicular }}{\text { hypotenuse }}$
$\sin
\theta=\frac{x^{2}-y^{2}}{x^{2}+y^{2}}$
$\Rightarrow
\frac{\mathrm{P}}{\mathrm{H}}=\frac{\mathrm{x}^{2}-\mathrm{y}^{2}}{\mathrm{x}^{2}+\mathrm{y}^{2}}$
$ \Rightarrow
\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{x}^{2}-\mathrm{y}^{2}}{\mathrm{x}^{2}+\mathrm{y}^{2}}$
Let,
Side opposite to angle θ = AB
= x2 – y2
and Hypotenuse = AC = x2 +
y2
In right angled ∆ABC, we have
(AB)2 + (BC)2 = (AC)2 [by using Pythagoras
theorem]
⇒ (x2 –
y2 )2 + (BC)2 = (x2 +
y2 )2
⇒ (BC)2 = (x2 + y2 )2 –
(x2 – y2 )2
Using the identity,
a2 – b2 = (a+b)(a – b)
⇒ (BC)2 = [(x2 + y2 + x2 –
y2 )][ x2 + y2 –( x2 –
y2)]
⇒ (BC)2 =
(2x2)(2y2)
⇒ (BC)2 = (4x2y2)
⇒ BC =√4x2y2
⇒ BC = ±2xy
⇒ BC = 2xy [taking positive
square root since, side cannot be negative]
$\therefore \cos \theta=\frac{\text { Base }}{\text {
Hypotenuse }}=\frac{\text { BC }}{\text { AC }}=\frac{2 x y}{x^{2}+y^{2}}$
and $\tan \theta=\frac{\text { Perpendicular }}{\text { Base
}}=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{x}^{2}-\mathrm{y}^{2}}{2 \mathrm{xy}}$
So, $\frac{1}{\tan \theta}=\frac{1}{\frac{x^{2}-y^{2}}{2 x y}}=\frac{2 x
y}{x^{2}-y^{2}}$
$\sin \theta=\frac{x^{2}-y^{2}}{x^{2}+v^{2}}$
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Or, $\sin \theta=\frac{\text { Perpendicular }}{\text { hypotenuse }}$
$\sin \theta=\frac{x^{2}-y^{2}}{x^{2}+y^{2}}$
Side opposite to angle θ = AB = x2 – y2
and Hypotenuse = AC = x2 + y2
In right angled ∆ABC, we have
(AB)2 + (BC)2 = (AC)2 [by using Pythagoras theorem]
⇒ (x2 – y2 )2 + (BC)2 = (x2 + y2 )2
⇒ (BC)2 = (x2 + y2 )2 – (x2 – y2 )2
Using the identity, a2 – b2 = (a+b)(a – b)
⇒ (BC)2 = [(x2 + y2 + x2 – y2 )][ x2 + y2 –( x2 – y2)]
⇒ (BC)2 = (2x2)(2y2)
⇒ (BC)2 = (4x2y2)
⇒ BC =√4x2y2
⇒ BC = ±2xy
⇒ BC = 2xy [taking positive square root since, side cannot be negative]
$\therefore \cos \theta=\frac{\text { Base }}{\text { Hypotenuse }}=\frac{\text { BC }}{\text { AC }}=\frac{2 x y}{x^{2}+y^{2}}$
and $\tan \theta=\frac{\text { Perpendicular }}{\text { Base }}=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{x}^{2}-\mathrm{y}^{2}}{2 \mathrm{xy}}$
So, $\frac{1}{\tan \theta}=\frac{1}{\frac{x^{2}-y^{2}}{2 x y}}=\frac{2 x y}{x^{2}-y^{2}}$
Question 21
Iftan
$\theta=\frac{\sqrt{\mathrm{m}^{2}-\mathrm{n}^{2}}}{\mathrm{n}}$, then find the values of sin θ and cos
θ.
Sol :
Given: $\tan
\theta=\frac{\sqrt{\mathrm{m}^{2}-\mathrm{n}^{2}}}{\mathrm{n}}$
We know that,
$\tan
\theta=\frac{\sqrt{\mathrm{m}^{2}-\mathrm{n}^{2}}}{\mathrm{n}} \Rightarrow
\frac{\mathrm{P}}{\mathrm{B}}=\frac{\sqrt{\mathrm{m}^{2}-\mathrm{n}^{2}}}{\mathrm{n}} \Rightarrow
\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\sqrt{\mathrm{m}^{2}-\mathrm{n}^{2}}}{\mathrm{n}}$
Let,
AB = √(m2 –
n2) and BC = n
In right angled ∆ABC, we have
(AB)2 + (BC)2 = (AC)2 [by using Pythagoras
theorem]
⇒ (√(m2 –
n2))2 + (n)2 = (AC )2
⇒ m2 – n2 + n2 = (AC
)2
⇒ (AC)2 =
(m2)
⇒ AC =√ m2
⇒ AC = ±m
⇒ AC = m [taking positive square root since, side cannot be
negative]
Now, we have to find the value of cos θ and sin θ
We, know that
$\cos \theta=\frac{\text { Base }}{\text { Hypotenuse
}}$
$=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{\mathrm{n}}{\mathrm{m}}$
and
$\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$=\frac{A
B}{A C}=\frac{\sqrt{m^{2}-n^{2}}}{m}$
Given: $\tan \theta=\frac{\sqrt{\mathrm{m}^{2}-\mathrm{n}^{2}}}{\mathrm{n}}$
$\tan \theta=\frac{\sqrt{\mathrm{m}^{2}-\mathrm{n}^{2}}}{\mathrm{n}} \Rightarrow \frac{\mathrm{P}}{\mathrm{B}}=\frac{\sqrt{\mathrm{m}^{2}-\mathrm{n}^{2}}}{\mathrm{n}} \Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\sqrt{\mathrm{m}^{2}-\mathrm{n}^{2}}}{\mathrm{n}}$
Let,
AB = √(m2 – n2) and BC = n
In right angled ∆ABC, we have
(AB)2 + (BC)2 = (AC)2 [by using Pythagoras theorem]
⇒ (√(m2 – n2))2 + (n)2 = (AC )2
⇒ m2 – n2 + n2 = (AC )2
⇒ (AC)2 = (m2)
⇒ AC =√ m2
⇒ AC = ±m
⇒ AC = m [taking positive square root since, side cannot be negative]
Now, we have to find the value of cos θ and sin θ
We, know that
$\cos \theta=\frac{\text { Base }}{\text { Hypotenuse }}$
$=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{\mathrm{n}}{\mathrm{m}}$
and
$\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$=\frac{A B}{A C}=\frac{\sqrt{m^{2}-n^{2}}}{m}$
Question 22 A
If sec θ = 2, then
find the values of other t–ratios of angle θ.
Sol
:
Given: sec θ = 2
We know that,
$\sec
\theta=\frac{\text { hypotenuse }}{\text { base }}$
$\operatorname{Sec} \theta=\frac{2}{1} \Rightarrow
\frac{\mathrm{H}}{\mathrm{B}}=\frac{2}{1} \Rightarrow
\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{2}{1}$
Let,
BC = 1k and AC =
2k
where, k is any positive integer.
In right angled ∆ABC, we have
(AB)2 + (BC)2 = (AC)2 [by using
Pythagoras theorem]
⇒ (AB)2 +
(1k)2 = (2k )2
⇒ (AB)2 +
k2 = 4k2
⇒ (AB)2 =
4k2 – k2
⇒ (AB)2 =
3k2
⇒ AB = k√3
Now, we have to find the value of other trigonometric
ratios.
We, know that
$\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse
}}$
$=\frac{A B}{A C}=\frac{k \sqrt{3}}{2 k}=\frac{\sqrt{3}}{2}$
$\cos \theta=\frac{\text {
Base }}{\text { Hypotenuse }}$
$=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{1 \mathrm{k}}{2
\mathrm{k}}=\frac{1}{2}$
$\tan \theta=\frac{\text { Perpendicular }}{\text { Base
}}$
$=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{k} \sqrt{3}}{1
\mathrm{k}}=\frac{\sqrt{3}}{1}=\sqrt{3}$
$\operatorname{cosec} \theta=\frac{1}{\sin
\theta}=\frac{1}{\frac{\sqrt{3}}{2}}=\frac{2}{\sqrt{3}}$
$\cot \theta=\frac{1}{\tan
\theta}=\frac{1}{\sqrt{3}}$
Given: sec θ = 2
$\sec \theta=\frac{\text { hypotenuse }}{\text { base }}$
$\operatorname{Sec} \theta=\frac{2}{1} \Rightarrow \frac{\mathrm{H}}{\mathrm{B}}=\frac{2}{1} \Rightarrow \frac{\mathrm{AC}}{\mathrm{BC}}=\frac{2}{1}$
Let,
BC = 1k and AC = 2k
where, k is any positive integer.
In right angled ∆ABC, we have
(AB)2 + (BC)2 = (AC)2 [by using Pythagoras theorem]
⇒ (AB)2 + (1k)2 = (2k )2
⇒ (AB)2 + k2 = 4k2
⇒ (AB)2 = 4k2 – k2
⇒ (AB)2 = 3k2
⇒ AB = k√3
Now, we have to find the value of other trigonometric ratios.
We, know that
$\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$=\frac{A B}{A C}=\frac{k \sqrt{3}}{2 k}=\frac{\sqrt{3}}{2}$
$\cos \theta=\frac{\text { Base }}{\text { Hypotenuse }}$
$=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{1 \mathrm{k}}{2 \mathrm{k}}=\frac{1}{2}$
$\tan \theta=\frac{\text { Perpendicular }}{\text { Base }}$
$=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{k} \sqrt{3}}{1 \mathrm{k}}=\frac{\sqrt{3}}{1}=\sqrt{3}$
$\operatorname{cosec} \theta=\frac{1}{\sin \theta}=\frac{1}{\frac{\sqrt{3}}{2}}=\frac{2}{\sqrt{3}}$
$\cot \theta=\frac{1}{\tan \theta}=\frac{1}{\sqrt{3}}$
Question 22 B
Given $\sec
\theta=\frac{13}{12}$ calculate all other trigonometric
ratios.
Sol
:
Given: $\sec \theta=\frac{13}{12}$
We know that,
$\sec \theta=\frac{\text { hypotenuse
}}{\text { base }}$
$\sec \theta=\frac{13}{12} \Rightarrow \frac{\mathrm{H}}{\mathrm{B}}=\frac{13}{12}
\Rightarrow \frac{\mathrm{AC}}{\mathrm{BC}}=\frac{13}{12}$
Let,
BC = 12k and AC =
13k
where, k is any positive integer.
In right angled ∆ABC, we have
(AB)2 + (BC)2 = (AC)2 [by using
Pythagoras theorem]
⇒ (AB)2 +
(12k)2 = (13k )2
⇒ (AB)2 +
144k2 = 169k2
⇒ (AB)2 =
169k2 – 144k2
⇒ (AB)2 =
25k2
⇒ AB = √25k2
⇒ AB =±5k [taking positive square root
since, side cannot be negative]
Now, we have to find the
value of other trigonometric ratios.
We, know
that
$\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$=\frac{A B}{A C}=\frac{5
k}{13 k}=\frac{5}{13}$
$\cos \theta=\frac{\text { Base }}{\text { Hypotenuse }}$
$=\frac{B C}{A
C}=\frac{12 k}{13 k}=\frac{12}{13}$
$\tan \theta=\frac{\text { Perpendicular }}{\text { Base
}}$
$=\frac{A B}{B C}=\frac{5 k}{12 k}=\frac{5}{12}$
$\operatorname{cosec} \theta=\frac{1}{\sin \theta}=\frac{1}{\frac{5}{13}}=\frac{13}{5}$
$\cot \theta=\frac{1}{\tan \theta}=\frac{1}{\frac{5}{12}}=\frac{12}{5}$
Question 23
If $\operatorname{cosec} \theta=\sqrt{10}$, then find the values of
other t–ratios of angle θ.
Sol :
Given: cosec θ =
√10
We know
that,
$\operatorname{cosec} \theta=\frac{\text { hypotenuse
}}{\text { perpendicular }}$
$\operatorname{cosec}
\theta=\frac{\sqrt{10}}{1} \Rightarrow \frac{\mathrm{H}}{\mathrm{P}}=\frac{\sqrt{10}}{1} \Rightarrow
\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\sqrt{10}}{1}$
Let,
AB = 1k and AC =
k√10
where, k is any positive
integer.
In right angled ∆ABC, we
have
(AB)2 + (BC)2 =
(AC)2 [by using Pythagoras theorem]
⇒ (1k )2+ (BC)2 = (k√10)2
⇒ (BC)2 = 10k2 – k2
⇒ (BC)2 = 9k2
⇒ BC = √9k2
⇒ BC =±3k [taking positive square root since, side cannot be negative]
Now, we have to find the value of other trigonometric
ratios.
We, know that
$\sin
\theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{1
\mathrm{k}}{\mathrm{k} \sqrt{10}}=\frac{1}{\sqrt{10}}$
$\cos \theta=\frac{\text { Base }}{\text {
Hypotenuse }}$
$=\frac{B C}{A C}=\frac{3 k}{k \sqrt{10}}=\frac{3}{\sqrt{10}}$
$\tan
\theta=\frac{\text { Perpendicular }}{\text { Base }}$
$=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{1
\mathrm{k}}{3 \mathrm{k}}=\frac{1}{3}$
$\sec \theta=\frac{1}{\cos
\theta}=\frac{1}{\frac{3}{\sqrt{10}}}=\frac{\sqrt{10}}{3}$
$\cot \theta=\frac{1}{\tan \theta}=\frac{1}{\frac{1}{3}}=3$
$\operatorname{cosec} \theta=\frac{\text { hypotenuse }}{\text { perpendicular }}$
$\operatorname{cosec} \theta=\frac{\sqrt{10}}{1} \Rightarrow \frac{\mathrm{H}}{\mathrm{P}}=\frac{\sqrt{10}}{1} \Rightarrow \frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\sqrt{10}}{1}$
Let,
AB = 1k and AC = k√10
where, k is any positive integer.
In right angled ∆ABC, we have
(AB)2 + (BC)2 = (AC)2 [by using Pythagoras theorem]
⇒ (1k )2+ (BC)2 = (k√10)2
⇒ (BC)2 = 10k2 – k2
⇒ (BC)2 = 9k2
⇒ BC = √9k2
⇒ BC =±3k [taking positive square root since, side cannot be negative]
Now, we have to find the value of other trigonometric ratios.
We, know that
$\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{1 \mathrm{k}}{\mathrm{k} \sqrt{10}}=\frac{1}{\sqrt{10}}$
$\cos \theta=\frac{\text { Base }}{\text { Hypotenuse }}$
$=\frac{B C}{A C}=\frac{3 k}{k \sqrt{10}}=\frac{3}{\sqrt{10}}$
$\tan \theta=\frac{\text { Perpendicular }}{\text { Base }}$
$=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{1 \mathrm{k}}{3 \mathrm{k}}=\frac{1}{3}$
Question 24 A
If $\tan
\mathrm{A}=\frac{\sqrt{3}}{2}$ then find the
values of sin A + cos A.
Sol
:
We know that,
$\tan
\theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle }
\theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
Given: $\tan
\mathrm{A}=\frac{\sqrt{3}}{2}$
$\Rightarrow \tan
\mathrm{A}=\frac{\sqrt{3}}{2}$
$\tan \mathrm{A}=\frac{\sqrt{3}}{2}
\Rightarrow \frac{\mathrm{P}}{\mathrm{B}}=\frac{\sqrt{3}}{2} \Rightarrow
\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{\sqrt{3}}{2}$
Let,
Side opposite to
angle A =BC = k√3
Side adjacent to
angle A =AB = 2k
where, k is any positive
integer
Firstly we have to find the value of
BC.
So, we can find the value of AC with the help of
Pythagoras theorem
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (2k)2 +
(√3k)2 = (AC)2
⇒ (AC)2 = 4 k2 +3 k2
⇒ (AC)2 = 7 k2
⇒ AC =√7 k2
⇒ AC =k√7
So, AC = k√7
Now, we will find the sin A and cos A
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse
}}$
Side opposite to angle A = BC = k√3
and
Hypotenuse = AC = k√7
So, $\sin \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{\mathrm{k}
\sqrt{3}}{\mathrm{k} \sqrt{7}}=\frac{\sqrt{3}}{\sqrt{7}}$
Now, we know that,
$\cos \theta=\frac{\text { side
adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent
to angle A = AB =2k
Hypotenuse = AC
= k√7
So, $\cos \mathrm{A}=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{2 \mathrm{k}}{\mathrm{k}
\sqrt{7}}=\frac{2}{\sqrt{7}}$
Now, we have to find sin
A +cos A
Putting values of sin A and cos A, we get
$\sin
\mathrm{A}+\cos \mathrm{A}=\frac{\sqrt{3}}{\sqrt{7}}+\frac{2}{\sqrt{7}}=\frac{\sqrt{3}+2}{\sqrt{7}}$
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
Given: $\tan \mathrm{A}=\frac{\sqrt{3}}{2}$
$\Rightarrow \tan \mathrm{A}=\frac{\sqrt{3}}{2}$
$\tan \mathrm{A}=\frac{\sqrt{3}}{2} \Rightarrow \frac{\mathrm{P}}{\mathrm{B}}=\frac{\sqrt{3}}{2} \Rightarrow \frac{\mathrm{BC}}{\mathrm{AB}}=\frac{\sqrt{3}}{2}$
Let,
Side opposite to angle A =BC = k√3
Side adjacent to angle A =AB = 2k
where, k is any positive integer
Firstly we have to find the value of BC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (2k)2 + (√3k)2 = (AC)2
⇒ (AC)2 = 4 k2 +3 k2
⇒ (AC)2 = 7 k2
⇒ AC =√7 k2
⇒ AC =k√7
So, AC = k√7
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle A = BC = k√3
and Hypotenuse = AC = k√7
So, $\sin \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{\mathrm{k} \sqrt{3}}{\mathrm{k} \sqrt{7}}=\frac{\sqrt{3}}{\sqrt{7}}$
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to angle A = AB =2k
Hypotenuse = AC = k√7
So, $\cos \mathrm{A}=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{2 \mathrm{k}}{\mathrm{k} \sqrt{7}}=\frac{2}{\sqrt{7}}$
Now, we have to find sin A +cos A
$\sin \mathrm{A}+\cos \mathrm{A}=\frac{\sqrt{3}}{\sqrt{7}}+\frac{2}{\sqrt{7}}=\frac{\sqrt{3}+2}{\sqrt{7}}$
Question 24 B
If $\sin
\theta=\sqrt{3} \cos \theta$ find the value of cos
θ – sin θ.
Sol :
Given: sin θ =√3cos
θ
$\Rightarrow \frac{\sin \theta}{\cos
\theta}=\sqrt{3}$
⇒ tan θ = √3
We know
that,
$\tan \theta=\frac{\text { side opposite to angle }
\theta}{\text { side adjacent to angle } \theta}$
Or $\tan \theta=\frac{\text {
perpendicular }}{\text { base }}$
Given: tan θ =
√3
$\Rightarrow \tan \theta=\frac{\sqrt{3}}{1}$
$\tan \theta=\frac{\sqrt{3}}{1} \Rightarrow
\frac{\mathrm{P}}{\mathrm{B}}=\frac{\sqrt{3}}{1} \Rightarrow
\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\sqrt{3}}{1}$
Let,
Side opposite to
angle θ =AC = √3k
Side adjacent to angle θ =AB =
1k
where k is any positive
integer
Firstly we have to find the value of
BC.
So, we can find the value of AC with the help of
Pythagoras theorem
⇒ (AB)2 +
(AC)2 = (BC)2
⇒ (1k)2 + (√3k)2 =
(BC)2
⇒ (BC)2 = 1
k2 +3 k2
⇒ (BC)2 = 4
k2
⇒ BC =√2
k2
⇒ BC =±2k
But side BC can’t be
negative. So, BC = 2k
Now, we will find
the sin B and cos B
$\sin \theta=\frac{\text { side opposite to
angle } \theta}{\text { hypotenuse }}$
Side opposite
to angle θ =
AC = k√3
and Hypotenuse = BC = 2k
So, $\sin
\theta=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{k} \sqrt{3}}{2
\mathrm{k}}=\frac{\sqrt{3}}{2}$
Now, we know
that,
$\cos \theta=\frac{\text { side adjacent to angle }
\theta}{\text { hypotenuse }}$
The side adjacent to
angle θ = AB =1k
Hypotenuse = BC
=2k
So, $\cos \theta=\frac{A B}{B C}=\frac{1 k}{2 k}=\frac{1}{2}$
Now, we have to find the value of cos θ – sin θ
Putting the values of sin θ and cos θ, we get
$\cos \theta-\sin \theta=\frac{1}{2}-\frac{\sqrt{3}}{2}=\frac{1-\sqrt{3}}{2}$
$\Rightarrow \frac{\sin \theta}{\cos \theta}=\sqrt{3}$
⇒ tan θ = √3
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
Given: tan θ = √3
$\Rightarrow \tan \theta=\frac{\sqrt{3}}{1}$
$\tan \theta=\frac{\sqrt{3}}{1} \Rightarrow \frac{\mathrm{P}}{\mathrm{B}}=\frac{\sqrt{3}}{1} \Rightarrow \frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\sqrt{3}}{1}$
Let,
Side opposite to angle θ =AC = √3k
Side adjacent to angle θ =AB = 1k
where k is any positive integer
Firstly we have to find the value of BC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (AC)2 = (BC)2
⇒ (1k)2 + (√3k)2 = (BC)2
⇒ (BC)2 = 1 k2 +3 k2
⇒ (BC)2 = 4 k2
⇒ BC =√2 k2
⇒ BC =±2k
But side BC can’t be negative. So, BC = 2k
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle θ = AC = k√3
and Hypotenuse = BC = 2k
So, $\sin \theta=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{k} \sqrt{3}}{2 \mathrm{k}}=\frac{\sqrt{3}}{2}$
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
The side adjacent to angle θ = AB =1k
Hypotenuse = BC =2k
So, $\cos \theta=\frac{A B}{B C}=\frac{1 k}{2 k}=\frac{1}{2}$
Now, we have to find the value of cos θ – sin θ
Putting the values of sin θ and cos θ, we get
$\cos \theta-\sin \theta=\frac{1}{2}-\frac{\sqrt{3}}{2}=\frac{1-\sqrt{3}}{2}$
Question 24 C
If $\tan \theta=\frac{8}{15}$, find the value of 1+
cos2 θ.
Sol
:
We know that,
$\tan
\theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle }
\theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
$\tan \theta=\frac{8}{15} \Rightarrow \frac{\mathrm{P}}{\mathrm{B}}=\frac{8}{15}
\Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{8}{15}$
Let,
Side opposite to
angle θ =AB = 8k
Side adjacent to
angle θ =BC = 15k
where, k is any positive
integer
Firstly we have to find the value of
AC.
So, we can find the value of AC with the help of
Pythagoras theorem
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (8k)2 +
(15k)2 = (AC)2
⇒ (AC)2 =
64k2+225k2
⇒ (AC)2 = 289
k2
⇒ AC =√289
k2
⇒ AC =±17k
But side AC can’t be
negative. So, AC = 17k
Now, we will find the cos
θ
We know that
$\cos
\theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to angle θ = BC = 15k
and
Hypotenuse = AC = 17k
So, $\cos \theta=\frac{B C}{A C}=\frac{15 k}{17 k}=\frac{15}{17}$
Now, we have to find the value of 1+
cos2 θ
Putting the value of cos θ, we get
$1+\cos ^{2} \theta=1+\left(\frac{15}{17}\right)^{2}$
$=1+\frac{225}{289}$
$=\frac{289+225}{289}$
$=\frac{514}{289}$
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
$\tan \theta=\frac{8}{15} \Rightarrow \frac{\mathrm{P}}{\mathrm{B}}=\frac{8}{15} \Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{8}{15}$
Let,
Side opposite to angle θ =AB = 8k
Side adjacent to angle θ =BC = 15k
where, k is any positive integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (8k)2 + (15k)2 = (AC)2
⇒ (AC)2 = 64k2+225k2
⇒ (AC)2 = 289 k2
⇒ AC =√289 k2
⇒ AC =±17k
But side AC can’t be negative. So, AC = 17k
Now, we will find the cos θ
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to angle θ = BC = 15k
and Hypotenuse = AC = 17k
So, $\cos \theta=\frac{B C}{A C}=\frac{15 k}{17 k}=\frac{15}{17}$
Now, we have to find the value of 1+ cos2 θ
$1+\cos ^{2} \theta=1+\left(\frac{15}{17}\right)^{2}$
Question 25
If $\cot \theta=\frac{7}{8}$, evaluate(i) $\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos
\theta)}$
(ii) $\cot ^{2} \theta$
Sol
:
Given: $\cot
\theta=\frac{7}{8}$
We know that,
$\cot \theta=\frac{\text { side adjacent to angle } \theta}{\text { side opposite to
angle } \theta}$
Or $\cot \theta=\frac{\text { base }}{\text { perpendicular }}$
$\cot \theta=\frac{7}{8} \Rightarrow \frac{\mathrm{B}}{\mathrm{P}}=\frac{7}{8}
\Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{7}{8}$
Let,
Side adjacent to
angle θ =AB = 7k
Side opposite to
angle θ =BC = 8k
where, k is any
positive integer
Firstly we have to find the value of
AC.
So, we can find the value of AC with the help of
Pythagoras theorem
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (7k)2 +
(8k)2 = (AC)2
⇒ (AC)2 = 49
k2 +69 k2
⇒ (AC)2 = 113
k2
⇒ AC =√113
k2
⇒ AC =k√113
$\therefore \sin
\theta=\frac{\mathrm{P}}{\mathrm{H}}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{8 \mathrm{k}}{\mathrm{k}
\sqrt{113}}=\frac{8}{\sqrt{113}}$
and $\cos \theta=\frac{B}{H}=\frac{A B}{A C}=\frac{7 k}{k
\sqrt{113}}=\frac{7}{\sqrt{113}}$
(i) $\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos
\theta)}$
We know that,
(a+b)(a – b) = (a2 – b2)
So, using this identity, we get
$=\frac{(1)^{2}-(\sin
\theta)^{2}}{(1)^{2}-(\cos \theta)^{2}}$
$=\frac{1-\sin ^{2} \theta}{1-\cos ^{2} \theta}$
$=\frac{1-\left(\frac{8}{\sqrt{113}}\right)^{2}}{1-\left(\frac{7}{\sqrt{113}}\right)^{2}}$
$=\frac{1-\frac{64}{113}}{1-\frac{49}{113}}$
$=\frac{\frac{113-64}{113}}{\frac{113-49}{113}}$
$=\frac{49}{64}$
(ii) cot2 θ
Given $\cot
\theta=\frac{7}{8}$
$=\left(\frac{7}{8}\right)^{2}$
$=\frac{49}{64}$
(ii) $\cot ^{2} \theta$
We know that,
$\cot \theta=\frac{\text { side adjacent to angle } \theta}{\text { side opposite to angle } \theta}$
Or $\cot \theta=\frac{\text { base }}{\text { perpendicular }}$
$\cot \theta=\frac{7}{8} \Rightarrow \frac{\mathrm{B}}{\mathrm{P}}=\frac{7}{8} \Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{7}{8}$
Let,
Side adjacent to angle θ =AB = 7k
Side opposite to angle θ =BC = 8k
where, k is any positive integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (7k)2 + (8k)2 = (AC)2
⇒ (AC)2 = 49 k2 +69 k2
⇒ (AC)2 = 113 k2
⇒ AC =√113 k2
⇒ AC =k√113
$\therefore \sin \theta=\frac{\mathrm{P}}{\mathrm{H}}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{8 \mathrm{k}}{\mathrm{k} \sqrt{113}}=\frac{8}{\sqrt{113}}$
(i) $\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}$
We know that,
(a+b)(a – b) = (a2 – b2)
So, using this identity, we get
$=\frac{(1)^{2}-(\sin \theta)^{2}}{(1)^{2}-(\cos \theta)^{2}}$
Given $\cot \theta=\frac{7}{8}$
Question 26 A
If 3 cot A = 4, check
whether $\frac{1-\tan ^{2} A}{1+\tan ^{2} A}$=cos2A–sin2 A or
not.
Sol
:
Given: 3cot A = 4
$\Rightarrow \cot A=\frac{4}{3}$
We know that,
$\cot \theta=\frac{\text { side adjacent
to angle } \theta}{\text { side opposite to angle } \theta}$
Or $\cot \theta=\frac{\text { base
}}{\text { perpendicular }}$
$\cot A=\frac{4}{3} \Rightarrow \frac{B}{P}=\frac{4}{3} \Rightarrow
\frac{A B}{B C}=\frac{4}{3}$
Let,
Side adjacent to angle A =AB = 4k
The side opposite to
angle A =BC = 3k
where k is any positive
integer
Firstly we have to find the value of
AC.
So, we can find the value of AC with the help of
Pythagoras theorem
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (4k)2 +
(3k)2 = (AC)2
⇒ (AC)2 = 16
k2 + 9 k2
⇒ (AC)2 = 25
k2
⇒ AC =√25k2
⇒ AC = ±5k [taking positive square root since, side cannot be
negative]
$\therefore \tan \mathrm{A}=\frac{1}{\cot
\mathrm{A}}=\frac{1}{\frac{4}{3}}=\frac{3}{4}$
$\sin
\mathrm{A}=\frac{\mathrm{P}}{\mathrm{H}}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3 \mathrm{k}}{5
\mathrm{k}}=\frac{3}{5}$
and $\cos A=\frac{B}{H}=\frac{A B}{A C}=\frac{4 k}{5
k}=\frac{4}{5}$
Now, $\mathrm{LHS}=\frac{1-\tan ^{2} \mathrm{A}}{1+\tan ^{2}
\mathrm{A}}=\frac{1-\left(\frac{3}{4}\right)^{2}}{1+\left(\frac{3}{4}\right)^{2}}$
$=\frac{1-\frac{9}{16}}{1+\frac{9}{16}}$
$=\frac{\frac{16-9}{16}}{\frac{16+9}{16}}$$=\frac{7}{25}$ …(i)
And RHS = cos2 A –
sin2 A
$=\left(\frac{4}{5}\right)^{2}-\left(\frac{3}{5}\right)^{2}$
$=\frac{16}{25}-\frac{9}{25}$
$=\frac{7}{25}$ …(ii)
From Eqs. (i) and (ii) LHS =RHS
Hence Proved
Given: 3cot A = 4
$\Rightarrow \cot A=\frac{4}{3}$
$\cot \theta=\frac{\text { side adjacent to angle } \theta}{\text { side opposite to angle } \theta}$
Or $\cot \theta=\frac{\text { base }}{\text { perpendicular }}$
$\cot A=\frac{4}{3} \Rightarrow \frac{B}{P}=\frac{4}{3} \Rightarrow \frac{A B}{B C}=\frac{4}{3}$
Let,
Side adjacent to angle A =AB = 4k
The side opposite to angle A =BC = 3k
where k is any positive integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (4k)2 + (3k)2 = (AC)2
⇒ (AC)2 = 16 k2 + 9 k2
⇒ (AC)2 = 25 k2
⇒ AC =√25k2
⇒ AC = ±5k [taking positive square root since, side cannot be negative]
$\therefore \tan \mathrm{A}=\frac{1}{\cot \mathrm{A}}=\frac{1}{\frac{4}{3}}=\frac{3}{4}$
$\sin \mathrm{A}=\frac{\mathrm{P}}{\mathrm{H}}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3 \mathrm{k}}{5 \mathrm{k}}=\frac{3}{5}$
and $\cos A=\frac{B}{H}=\frac{A B}{A C}=\frac{4 k}{5 k}=\frac{4}{5}$
Hence Proved
Question 26 B
In a right triangle
ABC, right angled at B, if tan A = 1, then verify that 2 sin A cos A = 1.
Sol
:
tan A = 1
As we know
$\tan \theta=\frac{\text {
perpedicular }}{\text { base }}$
Now construct a right
angle triangle right angled at B such that
∠ BAC = θ
Hence perpendicular =
BC = 1 and base = AB = 1
By Pythagoras theorem,
AC2 = AB2 + BC2
⇒ AC2 = (1)2 + (1)2
⇒ AC2 = 2
⇒ AC = 
As,
$\sin \theta=\frac{\text { perpendicular }}{\text { hypotenuse
}}$
and $\cos \theta=\frac{\text { base }}{\text {
hypotenuse }}$
⇒ $\sin \theta=\frac{1}{\sqrt{2}}$ and $\cos
\theta=\frac{1}{\sqrt{2}}$
Hence,
2 sin A cos A=$2 \times \frac{1}{\sqrt{2}} \times
\frac{1}{\sqrt{2}}$
⇒ 2 sin A cos A=$2 \times
\frac{1}{2}$
⇒ 2 sin A cos
A=1
= R.H.S
Hence proved.
tan A = 1
As we know
$\tan \theta=\frac{\text { perpedicular }}{\text { base }}$
Now construct a right angle triangle right angled at B such that
∠ BAC = θ
Hence perpendicular = BC = 1 and base = AB = 1
AC2 = AB2 + BC2
⇒ AC2 = (1)2 + (1)2
⇒ AC2 = 2
⇒ AC =
As,
and $\cos \theta=\frac{\text { base }}{\text { hypotenuse }}$
⇒ $\sin \theta=\frac{1}{\sqrt{2}}$ and $\cos \theta=\frac{1}{\sqrt{2}}$
Hence,
2 sin A cos A=$2 \times \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}$
⇒ 2 sin A cos A=$2 \times \frac{1}{2}$
⇒ 2 sin A cos A=1
= R.H.S
Hence proved.
Question 27
If
4sin2 θ =3 and 0o < θ <90o, find the value of 1 + cos
θ.
Sol
:
4sin2 θ =3
$\Rightarrow \sin ^{2}
\theta=\frac{3}{4}$
$\Rightarrow \sin \theta=\pm \frac{\sqrt{3}}{2}$
But it is given 0o< θ
<90o
So, $\sin \theta=\frac{\sqrt{3}}{2}$
$\sin \theta=\frac{\sqrt{3}}{2}
\Rightarrow \frac{\mathrm{P}}{\mathrm{H}}=\frac{\sqrt{3}}{2}$
Let, P =k√3 and H =2k
In right angled ∆ABC, we have
B2 + P2 = H2
⇒ B2 + (k√3)2 = (2k)2
⇒ B2 + 3k2 = 4k2
⇒ B2 = 4k2 – 3k2
⇒ B2 = k2
⇒ B = ±k
⇒ B = k [taking positive square root since, side cannot be
negative]
$\therefore \cos \theta=\frac{B}{H}=\frac{k}{2 k}=\frac{1}{2}$
So, $1+\cos
\theta=1+\frac{1}{2}=\frac{2+1}{2}=\frac{3}{2}$
4sin2 θ =3
$\Rightarrow \sin ^{2} \theta=\frac{3}{4}$
$\Rightarrow \sin \theta=\pm \frac{\sqrt{3}}{2}$
So, $\sin \theta=\frac{\sqrt{3}}{2}$
$\sin \theta=\frac{\sqrt{3}}{2} \Rightarrow \frac{\mathrm{P}}{\mathrm{H}}=\frac{\sqrt{3}}{2}$
In right angled ∆ABC, we have
B2 + P2 = H2
⇒ B2 + (k√3)2 = (2k)2
⇒ B2 + 3k2 = 4k2
⇒ B2 = 4k2 – 3k2
⇒ B2 = k2
⇒ B = ±k
⇒ B = k [taking positive square root since, side cannot be negative]
$\therefore \cos \theta=\frac{B}{H}=\frac{k}{2 k}=\frac{1}{2}$
So, $1+\cos \theta=1+\frac{1}{2}=\frac{2+1}{2}=\frac{3}{2}$
Question 28
If $\tan \theta=\frac{p}{q}$find the value of $\frac{p \sin \theta-q \cos \theta}{p \sin \theta+q
\cos \theta}$.
Sol
:
Given:$\tan \theta=\frac{p}{q}$
Now, $\frac{p \sin
\theta-q \cos \theta}{p \sin \theta+q \cos \theta}$
$\Rightarrow
\frac{\cos \theta\left(\frac{p \sin \theta}{\cos \theta}-q\right)}{\cos \theta\left(\frac{p \sin \theta}{\cos
\theta}+q\right)}$
$\Rightarrow \frac{p \tan \theta-q}{p \tan \theta+q}$ $\left[\because \tan
\theta=\frac{\sin \theta}{\cos \theta}\right]$
$\Rightarrow
\frac{p\left(\frac{p}{q}\right)-q}{p\left(\frac{p}{q}\right)+q}$
$\Rightarrow
\frac{\frac{p^{2}-q^{2}}{q}}{\frac{p^{2}+q^{2}}{q}}$
$\Rightarrow
\frac{p^{2}-q^{2}}{p^{2}+q^{2}}$
$\therefore \frac{p \sin \theta-q \cos \theta}{p \sin \theta+q \cos
\theta}=\frac{p^{2}-q^{2}}{p^{2}+q^{2}}$
Given:$\tan \theta=\frac{p}{q}$
$\Rightarrow \frac{\cos \theta\left(\frac{p \sin \theta}{\cos \theta}-q\right)}{\cos \theta\left(\frac{p \sin \theta}{\cos \theta}+q\right)}$
$\Rightarrow \frac{p\left(\frac{p}{q}\right)-q}{p\left(\frac{p}{q}\right)+q}$
$\Rightarrow \frac{\frac{p^{2}-q^{2}}{q}}{\frac{p^{2}+q^{2}}{q}}$
$\Rightarrow \frac{p^{2}-q^{2}}{p^{2}+q^{2}}$
$\therefore \frac{p \sin \theta-q \cos \theta}{p \sin \theta+q \cos \theta}=\frac{p^{2}-q^{2}}{p^{2}+q^{2}}$
Question 29
If 13 cos θ =
5, $\frac{\sin \theta+\cos \theta}{\sin \theta-\cos \theta}$.
Sol
:
Given: 13 cosθ = 5
$\Rightarrow \cos
\theta=\frac{5}{13}$
We know that,
$\cos \theta=\frac{\text { Base }}{\text
{ hypotenuse }}$
$\cos \theta=\frac{5}{13} \Rightarrow \frac{B}{H}=\frac{5}{13}$
Let AB =5k and BC = 13k
In right angled ∆ABC, we have
B2 + P2 = H2
⇒ (5k)2 + P2 = (13k)2
⇒ P2 + 25k2 = 169k2
⇒ P2 = 169k2 – 25k2
⇒ P2 = 144k2
⇒ P =√144k2
⇒ P = ±12k
⇒ P = 12k [taking positive square root since, side cannot be
negative]
$\therefore \sin \theta=\frac{P}{H}=\frac{12}{13}$
Now, $\frac{\sin
\theta+\cos \theta}{\sin \theta-\cos
\theta}$
$=\frac{\frac{12}{13}+\frac{5}{13}}{\frac{12}{13}-\frac{5}{13}}$
$=\frac{17}{7}$
Given: 13 cosθ = 5
$\Rightarrow \cos \theta=\frac{5}{13}$
$\cos \theta=\frac{\text { Base }}{\text { hypotenuse }}$
$\cos \theta=\frac{5}{13} \Rightarrow \frac{B}{H}=\frac{5}{13}$
Let AB =5k and BC = 13k
In right angled ∆ABC, we have
B2 + P2 = H2
⇒ (5k)2 + P2 = (13k)2
⇒ P2 + 25k2 = 169k2
⇒ P2 = 169k2 – 25k2
⇒ P2 = 144k2
⇒ P =√144k2
⇒ P = ±12k
⇒ P = 12k [taking positive square root since, side cannot be negative]
$\therefore \sin \theta=\frac{P}{H}=\frac{12}{13}$
Now, $\frac{\sin \theta+\cos \theta}{\sin \theta-\cos \theta}$
$=\frac{\frac{12}{13}+\frac{5}{13}}{\frac{12}{13}-\frac{5}{13}}$
$=\frac{17}{7}$
Question 30
If $\sec \theta=\frac{13}{5}$, show that $\frac{2 \sin
\theta-3 \cos \theta}{4 \sin \theta-9 \cos \theta}=3$.Sol :
Given:
$\sec \theta=\frac{13}{5}$
We know that,
$\sec \theta=\frac{\text { hypotenuse
}}{\text { base }}$
$\operatorname{Sec} \theta=\frac{13}{5} \Rightarrow
\frac{\mathrm{H}}{\mathrm{B}}=\frac{13}{5} \Rightarrow \frac{\mathrm{AC}}{\mathrm{BC}}=\frac{13}{5}$
Let,
BC = 5k and
AC = 13k
where, k is any positive
integer.
In right angled ∆ABC, we
have
(AB)2 + (BC)2 =
(AC)2 [by using Pythagoras theorem]
⇒ (AB)2 + (5k)2 = (13k )2
⇒ (AB)2 + 25k2 = 169k2
⇒ (AB)2 = 169k2 – 25k2
⇒ (AB)2 = 144k2
⇒ AB = √144k2
⇒ AB =±12k [taking positive square root since, side cannot be negative]
Now, we have to find the value of other trigonometric
ratios.
We, know that
$\sin
\theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$=\frac{A B}{A C}=\frac{12 k}{13
k}=\frac{12}{13}$
$\cos \theta=\frac{\text { Base }}{\text { Hypotenuse }}$
$=\frac{B C}{A
C}=\frac{5 k}{13 k}=\frac{5}{13}$
Now, LHS $=\frac{2 \sin \theta-3 \cos \theta}{4 \sin \theta-9
\cos
\theta}$
$=\frac{2\left(\frac{12}{13}\right)-3\left(\frac{5}{13}\right)}{4\left(\frac{12}{13}\right)-9\left(\frac{5}{13}\right)}$
$=\frac{24-15}{48-45}$
$=\frac{9}{3}$=3 =RHS
Hence Proved
Given:
$\sec \theta=\frac{\text { hypotenuse }}{\text { base }}$
$\operatorname{Sec} \theta=\frac{13}{5} \Rightarrow \frac{\mathrm{H}}{\mathrm{B}}=\frac{13}{5} \Rightarrow \frac{\mathrm{AC}}{\mathrm{BC}}=\frac{13}{5}$
Let,
BC = 5k and AC = 13k
where, k is any positive integer.
In right angled ∆ABC, we have
(AB)2 + (BC)2 = (AC)2 [by using Pythagoras theorem]
⇒ (AB)2 + (5k)2 = (13k )2
⇒ (AB)2 + 25k2 = 169k2
⇒ (AB)2 = 169k2 – 25k2
⇒ (AB)2 = 144k2
⇒ AB = √144k2
⇒ AB =±12k [taking positive square root since, side cannot be negative]
Now, we have to find the value of other trigonometric ratios.
We, know that
$\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$=\frac{A B}{A C}=\frac{12 k}{13 k}=\frac{12}{13}$
$\cos \theta=\frac{\text { Base }}{\text { Hypotenuse }}$
$=\frac{B C}{A C}=\frac{5 k}{13 k}=\frac{5}{13}$
$=\frac{2\left(\frac{12}{13}\right)-3\left(\frac{5}{13}\right)}{4\left(\frac{12}{13}\right)-9\left(\frac{5}{13}\right)}$
Hence Proved
Question 31
If 2 tan θ = 1, find
the value of $\frac{3 \cos \theta+\sin \theta}{2 \cos \theta-\sin \theta}$.
Sol
:
Given: 2 tan θ = 1
$\Rightarrow \tan
\theta=\frac{1}{2}$
We know that,
$\tan \theta=\frac{\text { side opposite
to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan \theta=\frac{\text {
perpendicular }}{\text { base }}$
$\tan \theta=\frac{1}{2} \Rightarrow
\frac{\mathrm{P}}{\mathrm{B}}=\frac{1}{2} \Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{1}{2}$
Let,
Side opposite to angle θ =AB = 1k
Side adjacent to
angle θ =BC = 2k
where, k is any
positive integer
Firstly we have to find the value of
AC.
So, we can find the value of AC with the help of
Pythagoras theorem
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (k)2 +
(2k)2 = (AC)2
⇒ (AC)2 =
k2+4k2
⇒ (AC)2 =
5k2
⇒ AC =√5k2
⇒ AC =±k√5
But side AC can’t be negative. So, AC = k√5
Now, we will find the sin θ and cos θ
Given: 2 tan θ = 1
$\Rightarrow \tan \theta=\frac{1}{2}$
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
$\tan \theta=\frac{1}{2} \Rightarrow \frac{\mathrm{P}}{\mathrm{B}}=\frac{1}{2} \Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{1}{2}$
Let,
Side opposite to angle θ =AB = 1k
Side adjacent to angle θ =BC = 2k
where, k is any positive integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (k)2 + (2k)2 = (AC)2
⇒ (AC)2 = k2+4k2
⇒ (AC)2 = 5k2
⇒ AC =√5k2
⇒ AC =±k√5
But side AC can’t be negative. So, AC = k√5
We know that
$\cos \theta=\frac{\text { side adjacent to
angle } \theta}{\text { hypotenuse }}$
Side adjacent to
angle θ = BC =
2k
and Hypotenuse = AC = k√5
So,$\cos \theta=\frac{B C}{A C}=\frac{2 k}{k
\sqrt{5}}=\frac{2}{\sqrt{5}}$
And $\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse
}}$
Side adjacent to angle θ =AB = 1k
And Hypotenuse =AC = k√5
So, $\sin \theta=\frac{A B}{A
C}=\frac{1 k}{k \sqrt{5}}=\frac{1}{\sqrt{5}}$
Now, $\frac{3 \cos \theta+\sin \theta}{2
\cos \theta-\sin
\theta}$
$=\frac{3\left(\frac{2}{\sqrt{5}}\right)+\frac{1}{\sqrt{5}}}{2\left(\frac{2}{\sqrt{5}}\right)-\frac{1}{\sqrt{5}}}$
$=\frac{6+1}{4-1}$
$=\frac{7}{3}$
Question 32
If 5 tan α = 4, show
that $\frac{5 \sin \alpha-3 \cos \alpha}{5 \sin \alpha+2 \cos
\alpha}=\frac{1}{6}$.
Sol
:
Given: 5 tan = 4
$\Rightarrow \tan \alpha=\frac{4}{5}$
We know that,
$\tan \theta=\frac{\text { side opposite
to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan \theta=\frac{\text {
perpendicular }}{\text { base }}$
$\tan \alpha=\frac{4}{5} \Rightarrow
\frac{\mathrm{P}}{\mathrm{B}}=\frac{4}{5} \Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{4}{5}$
Let,
The side opposite to angle α =AB = 4k
The side adjacent to
angle α =BC = 5k
where k is any positive
integer
Firstly we have to find the value of
AC.
So, we can find the value of AC with the help of
Pythagoras theorem
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (4k)2 +
(5k)2 = (AC)2
⇒ (AC)2 =
16k2+25k2
⇒ (AC)2 =
41k2
⇒ AC =√41k2
⇒ AC =±k√41
But side AC can’t be negative. So, AC = k√41
Now, we will find the sin α and cos α
We know that
$\cos \theta=\frac{\text { side adjacent to angle }
\theta}{\text { hypotenuse }}$
Side adjacent to
angle α = BC =
5k
and Hypotenuse = AC = k√41
So, $\cos
\alpha=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{5 \mathrm{k}}{\mathrm{k}
\sqrt{41}}=\frac{5}{\sqrt{41}}$
And $\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse
}}$
Side adjacent to angle α =AB = 4k
And Hypotenuse =AC = k√5
So, $\sin \alpha=\frac{A B}{A
C}=\frac{4 k}{k \sqrt{4} 1}=\frac{4}{\sqrt{41}}$
Now, LHS $=\frac{5
\sin \alpha-3 \cos \alpha}{5 \sin \alpha+2 \cos
\alpha}$
$=\frac{5\left(\frac{4}{\sqrt{41}}\right)-3\left(\frac{5}{\sqrt{41}}\right)}{5\left(\frac{4}{\sqrt{41}}\right)+2\left(\frac{5}{\sqrt{41}}\right)}$
$=\frac{20-15}{20+10}$
$=\frac{5}{30}$
$=\frac{1}{6}$
=
RHS
Hence Proved
Given: 5 tan = 4
$\Rightarrow \tan \alpha=\frac{4}{5}$
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to angle } \theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
$\tan \alpha=\frac{4}{5} \Rightarrow \frac{\mathrm{P}}{\mathrm{B}}=\frac{4}{5} \Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{4}{5}$
Let,
The side opposite to angle α =AB = 4k
The side adjacent to angle α =BC = 5k
where k is any positive integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (4k)2 + (5k)2 = (AC)2
⇒ (AC)2 = 16k2+25k2
⇒ (AC)2 = 41k2
⇒ AC =√41k2
⇒ AC =±k√41
But side AC can’t be negative. So, AC = k√41
Now, we will find the sin α and cos α
We know that
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to angle α = BC = 5k
and Hypotenuse = AC = k√41
So, $\cos \alpha=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{5 \mathrm{k}}{\mathrm{k} \sqrt{41}}=\frac{5}{\sqrt{41}}$
And $\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side adjacent to angle α =AB = 4k
And Hypotenuse =AC = k√5
So, $\sin \alpha=\frac{A B}{A C}=\frac{4 k}{k \sqrt{4} 1}=\frac{4}{\sqrt{41}}$
$=\frac{5\left(\frac{4}{\sqrt{41}}\right)-3\left(\frac{5}{\sqrt{41}}\right)}{5\left(\frac{4}{\sqrt{41}}\right)+2\left(\frac{5}{\sqrt{41}}\right)}$
$=\frac{20-15}{20+10}$
Hence Proved
Question 33
If $\cot \theta=\frac{3}{4}$prove that $\sqrt{\frac{\sec \theta+\operatorname{cosec}
\theta}{\sec \theta-\operatorname{cosec} \theta}}=\sqrt{7}$.
Sol
:
We know that,
$\cot
\theta=\frac{\text { side adjacent to angle } \theta}{\text { side opposite to angle }
\theta}$
Or $\cot \theta=\frac{\text { base }}{\text { perpendicular }}$
$\cot \theta=\frac{3}{4} \Rightarrow \frac{\mathrm{B}}{\mathrm{P}}=\frac{3}{4}
\Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{3}{4}$
Let,
Side adjacent to
angle θ =AB = 3k
The side opposite to
angle θ =BC = 4k
where k is any positive
integer
Firstly we have to find the value of
AC.
So, we can find the value of AC with the help of
Pythagoras theorem
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (3k)2 +
(4k)2 = (AC)2
⇒ (AC)2 =
9k2 +16k2
⇒ (AC)2 =
25k2
⇒ AC =√25k2
⇒ AC =±5k
But side AC can’t be negative. So, AC = 5k
Now, we will find the sin θ
$\sin \theta=\frac{\text {
side opposite to angle } \theta}{\text { hypotenuse }}$
Side
opposite to angle θ = BC = 4k
and Hypotenuse =
AC = 5k
So, $\sin \theta=\frac{B C}{A C}=\frac{4 k}{5 k}=\frac{4}{5}$
Now, we know that,
$\cos \theta=\frac{\text { side
adjacent to angle } \theta}{\text { hypotenuse }}$
The side
adjacent to angle θ = AB =3k
Hypotenuse = AC
=5k
So, $\cos \theta=\frac{A B}{A C}=\frac{3 k}{5
k}=\frac{3}{5}$
$\therefore \sec \theta=\frac{1}{\cos
\theta}=\frac{1}{\frac{3}{5}}=\frac{5}{3}$
And
$\operatorname{cosec} \theta=\frac{1}{\sin
\theta}=\frac{1}{\frac{4}{5}}=\frac{5}{4}$
Now, LHS$=\sqrt{\frac{\sec
\theta+\operatorname{cosec} \theta}{\sec \theta-\operatorname{cosec} \theta}}$
$=\sqrt{\frac{\left(\frac{5}{3}\right)+\left(\frac{5}{4}\right)}{\left(\frac{5}{3}\right)-\left(\frac{5}{4}\right)}}$
$=\sqrt{\frac{\left(\frac{20+15}{12}\right)}{\left(\frac{20-15}{12}\right)}}$
$=\sqrt{\frac{35}{5}}$$=\sqrt{7}$ = RHS
Hence
Proved
$\cot \theta=\frac{\text { side adjacent to angle } \theta}{\text { side opposite to angle } \theta}$
Or $\cot \theta=\frac{\text { base }}{\text { perpendicular }}$
$\cot \theta=\frac{3}{4} \Rightarrow \frac{\mathrm{B}}{\mathrm{P}}=\frac{3}{4} \Rightarrow \frac{\mathrm{AB}}{\mathrm{BC}}=\frac{3}{4}$
Let,
Side adjacent to angle θ =AB = 3k
The side opposite to angle θ =BC = 4k
where k is any positive integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (3k)2 + (4k)2 = (AC)2
⇒ (AC)2 = 9k2 +16k2
⇒ (AC)2 = 25k2
⇒ AC =√25k2
⇒ AC =±5k
But side AC can’t be negative. So, AC = 5k
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle θ = BC = 4k
and Hypotenuse = AC = 5k
So, $\sin \theta=\frac{B C}{A C}=\frac{4 k}{5 k}=\frac{4}{5}$
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
The side adjacent to angle θ = AB =3k
Hypotenuse = AC =5k
So, $\cos \theta=\frac{A B}{A C}=\frac{3 k}{5 k}=\frac{3}{5}$
$\therefore \sec \theta=\frac{1}{\cos \theta}=\frac{1}{\frac{3}{5}}=\frac{5}{3}$
And
$\operatorname{cosec} \theta=\frac{1}{\sin \theta}=\frac{1}{\frac{4}{5}}=\frac{5}{4}$
Hence Proved
Question 34
If $\cot \theta=\frac{1}{\sqrt{3}}$ verify
that: $\frac{1-\cos ^{2} \theta}{2-\sin ^{2} \theta}=\frac{3}{5}$.
Sol
:
We know that,
$\cot \theta=\frac{\text { side adjacent
to angle } \theta}{\text { side opposite to angle } \theta}$
Or $\cot \theta=\frac{\text { base
}}{\text { perpendicular }}$
$\cot \theta=\frac{1}{\sqrt{3}} \Rightarrow
\frac{\mathrm{B}}{\mathrm{P}}=\frac{1}{\sqrt{3}} \Rightarrow \frac{\mathrm{AB}}{\mathrm{AC}}=\frac{1}{\sqrt{3}}$
Let,
Side adjacent to angle θ =AB = 1k
Side opposite to
angle θ =AC = k√3
where, k is any
positive integer
Firstly we have to find the value of
BC.
So, we can find the value of AC with the help of
Pythagoras theorem
⇒ (AB)2 +
(AC)2 = (BC)2
⇒ (1k)2 +
(√3k)2 = (BC)2
⇒ (BC)2 = 1 k2 +3 k2
⇒ (BC)2 = 4 k2
⇒ BC =√2 k2
⇒ BC =±2k
But side BC can’t be negative. So, BC = 2k
Now, we will find the sin θ and cos θ
$\sin \theta=\frac{\text { side
opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite
to angle θ = AC
= k√3
and Hypotenuse = BC = 2k
So$\sin \theta=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{k} \sqrt{3}}{2
\mathrm{k}}=\frac{\sqrt{3}}{2}$
Now, we know that,
$\cos \theta=\frac{\text { side
adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent
to angle θ = AB =1k
Hypotenuse = BC
=2k
So, $\cos \theta=\frac{A B}{B C}=\frac{1 k}{2 k}=\frac{1}{2}$
Now, LHS $=\frac{1-\cos ^{2} \theta}{2-\sin ^{2}
\theta}$
$=\frac{1-\left(\frac{1}{2}\right)^{2}}{2-\left(\frac{\sqrt{3}}{2}\right)^{2}}$
$=\frac{1-\frac{1}{4}}{2-\frac{3}{4}}$
$=\frac{\frac{4-1}{4}}{\frac{8-3}{4}}$
$=\frac{3}{5}$ =
RHS
Hence Proved
$\cot \theta=\frac{\text { side adjacent to angle } \theta}{\text { side opposite to angle } \theta}$
Or $\cot \theta=\frac{\text { base }}{\text { perpendicular }}$
$\cot \theta=\frac{1}{\sqrt{3}} \Rightarrow \frac{\mathrm{B}}{\mathrm{P}}=\frac{1}{\sqrt{3}} \Rightarrow \frac{\mathrm{AB}}{\mathrm{AC}}=\frac{1}{\sqrt{3}}$
Let,
Side adjacent to angle θ =AB = 1k
Side opposite to angle θ =AC = k√3
where, k is any positive integer
Firstly we have to find the value of BC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (AC)2 = (BC)2
⇒ (1k)2 + (√3k)2 = (BC)2
⇒ (BC)2 = 1 k2 +3 k2
⇒ (BC)2 = 4 k2
⇒ BC =√2 k2
⇒ BC =±2k
But side BC can’t be negative. So, BC = 2k
Now, we will find the sin θ and cos θ
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to angle θ = AC = k√3
and Hypotenuse = BC = 2k
So$\sin \theta=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{k} \sqrt{3}}{2 \mathrm{k}}=\frac{\sqrt{3}}{2}$
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to angle θ = AB =1k
Hypotenuse = BC =2k
So, $\cos \theta=\frac{A B}{B C}=\frac{1 k}{2 k}=\frac{1}{2}$
$=\frac{1-\left(\frac{1}{2}\right)^{2}}{2-\left(\frac{\sqrt{3}}{2}\right)^{2}}$
$=\frac{1-\frac{1}{4}}{2-\frac{3}{4}}$
$=\frac{\frac{4-1}{4}}{\frac{8-3}{4}}$
$=\frac{3}{5}$ = RHS
Hence Proved
Question 35
If $\tan
\theta=\frac{x}{y}$ find the value of x sin θ + y
cos θ.
Sol
:
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent
to angle } \theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
$\tan \theta=\frac{x}{y} \Rightarrow \frac{P}{B}=\frac{x}{y} \Rightarrow \frac{A B}{B
C}=\frac{x}{y}$
Let,
Side opposite to angle θ =AB = x
Side adjacent to angle θ =BC = y
where, k is any positive integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras theorem
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (x)2 + (y)2 = (AC)2
⇒ (AC)2 = x2+y2
⇒ AC =√( x2+y2)
Now, we will find the sin θ and cos θ
We know that
$\cos \theta=\frac{\text { side
adjacent to angle } \theta}{\text { hypotenuse }}$
Side
adjacent to angle θ = BC = y
and Hypotenuse = AC
= √( x2+y2)
So,$\cos \theta=\frac{B
C}{A C}=\frac{y}{\sqrt{x^{2}+y^{2}}}$
And $\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse
}}$
Side adjacent to angle θ =AB = x
And Hypotenuse =AC = √(
x2+y2)
So, $\sin
\theta=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{x}}{\sqrt{\mathrm{x}^{2}+\mathrm{y}^{2}}}$
Now, x sin θ +y cos
θ
$=\mathrm{x}\left(\frac{\mathrm{x}}{\sqrt{\mathrm{x}^{2}+\mathrm{y}^{2}}}\right)+\mathrm{y}\left(\frac{\mathrm{y}}{\sqrt{\mathrm{x}^{2}+\mathrm{y}^{2}}}\right)$
$=\frac{x^{2}+y^{2}}{\sqrt{x^{2}+y^{2}}}$
= √( x2+y2)
Question 36
If $\sin \theta=\frac{3}{5}$, find the value of tan2θ
+ sinθ cosθ + cotθ.
Sol :
Given: $\sin \theta=\frac{3}{5}$
We know that,
$\sin \theta=\frac{\text { side opposite
to angle } \theta}{\text { hypotenuse }}$
Or $\sin \theta=\frac{\text {
Perpendicular }}{\text { Hypollyuse }}$
$\sin \theta=\frac{3}{5} \Rightarrow
\frac{\mathrm{P}}{\mathrm{H}}=\frac{3}{5} \Rightarrow \frac{\mathrm{AB}}{\mathrm{AC}}=\frac{3}{5}$
Let,
Perpendicular =AB =3k
and
Hypotenuse =AC =5k
where, k is any positive integer
So, by Pythagoras theorem, we can find the third side of a triangle
In right angled ∆ ABC, we
have
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (3k)2 + (BC)2 = (5k)2
⇒ 9k2 + (BC)2 =
25k2
⇒ (BC)2 = 25
k2 –9k2
⇒ (BC)2 = 16k2
⇒ BC =√16k2
⇒ BC =±4k
But side BC can’t be negative. So, BC = 4k
Now, we have to find the value of cos θ and tan θ
We know
that,
$\cos \theta=\frac{\text { base }}{\text { hypotenuse }}$
The side
adjacent to angle θ or base = BC
=4k
Hypotenuse = AC =5k
So,$\cos \theta=\frac{4
k}{5 k}=\frac{4}{5}$
Now,
We know
that,
$\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
Perpendicular = AB =3k
Base = BC =4k
So, $\tan \theta=\frac{3 \mathrm{k}}{4 \mathrm{k}}=\frac{3}{4}$
$\cot
\theta=\frac{1}{\tan \theta}=\frac{1}{\frac{3}{4}}=\frac{4}{3}$
Now, tan2 θ + sin θ cos θ + cot θ
$=\left(\frac{3}{4}\right)^{2}+\left(\frac{3}{5}\right)\left(\frac{4}{5}\right)+\left(\frac{4}{3}\right)$
$=\left(\frac{9}{16}\right)+\left(\frac{13}{25}\right)+\left(\frac{4}{3}\right)$
$=\frac{675+576+1600}{16 \times 25 \times 3}$
$=\frac{2851}{1200}$
Question 37
If 4cot θ = 3, show
that $\frac{\sin \theta+\cos \theta}{\sin \theta-\cos \theta}=7$.
Sol :
Given: $\cot \theta=\frac{3}{4}$
We know that,
$\cot \theta=\frac{\text { side adjacent to angle } \theta}{\text { side opposite to
angle } \theta}$
Or $\cot \theta=\frac{\text { base }}{\text { perpendicular
}}$
$\cot \theta=\frac{3}{4} \Rightarrow \frac{\mathrm{B}}{\mathrm{P}}=\frac{3}{4} \Rightarrow
\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{3}{4}$
Let,
Side
adjacent to angle θ =AB = 3k
The side opposite to angle θ =BC = 4k
where k is any positive integer
Firstly we have to find the value of
AC.
So, we can find the value of AC with the help of Pythagoras
theorem
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (3k)2 + (4k)2 = (AC)2
⇒ (AC)2 =
9k2 +16k2
⇒ (AC)2 = 25k2
⇒ AC =√25k2
⇒ AC =±5k
But side AC can’t be negative. So, AC = 5k
Now, we will find the sin θ
$\sin \theta=\frac{\text {
side opposite to angle } \theta}{\text { hypotenuse }}$
Side opposite to
angle θ = BC = 4k
and Hypotenuse = AC =
5k
So, $\sin \theta=\frac{B C}{A C}=\frac{4 k}{5
k}=\frac{4}{5}$
Now, we know that,
$\cos \theta=\frac{\text { side
adjacent to angle } \theta}{\text { hypotenuse }}$
Side adjacent to
angle θ = AB =3k
Hypotenuse = AC =5k
So, $\cos \theta=\frac{A B}{A
C}=\frac{3 k}{5 k}=\frac{3}{5}$
Now, LHS $=\frac{\sin \theta+\cos \theta}{\sin
\theta-\cos \theta}$
$=\frac{\frac{4}{5}+\frac{3}{5}}{\frac{4}{5}-\frac{3}{5}}$
$=\frac{7}{1}$
= 7 = RHS
Hence Proved
Question 38
If $\sin \theta=\frac{\mathrm{m}}{\sqrt{\mathrm{m}^{2}+\mathrm{n}^{2}}}$, prove
that $\mathrm{m} \sin \theta+\mathrm{n} \cos
\theta=\sqrt{\mathrm{m}^{2}+\mathrm{n}^{2}}$
Sol :
Given: $\sin
\theta=\frac{\mathrm{m}}{\sqrt{\mathrm{m}^{2}+\mathrm{n}^{2}}}$
We know that,
$\sin \theta=\frac{\text { side opposite
to angle } \theta}{\text { hypotenuse }}$
Or $\sin \theta=\frac{\text {
Perpendicular }}{\text { Hypotenuse }}$
$\sin \theta=\frac{\mathrm{m}}{\sqrt{\mathrm{m}^{2}+\mathrm{n}^{2}}}
\Rightarrow \frac{\mathrm{P}}{\mathrm{H}}=\frac{\mathrm{m}}{\sqrt{\mathrm{m}^{2}+\mathrm{n}^{2}}} \Rightarrow
\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{m}}{\sqrt{\mathrm{m}^{2}+\mathrm{n}^{2}}}$
Let,
Perpendicular =AB
=m
and Hypotenuse =AC =√(m2 +
n2)
where, k is any positive integer
So, by Pythagoras theorem, we can find the third side of a triangle
In right angled ∆ ABC, we
have
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (m)2 + (BC)2 = (√(m2 +
n2))2
⇒ m2 + (BC)2 = m2 +
n2
⇒ (BC)2 = m2 + n2 –
m2
⇒ (BC)2 =
n2
⇒ BC =√n2
⇒ BC =±n
But side BC can’t be negative. So, BC = n
Now, we have to find the value of cos θ and tan θ
We know that,
$\cos \theta=\frac{\text { base }}{\text {
hypotenuse }}$
Side adjacent to angle θ or
base = BC =n
Hypotenuse = AC =√(m2 + n2)
So, $\cos \theta=\frac{n}{\sqrt{m^{2}+n^{2}}}$
Now, LHS = m sin θ +n
cosθ
$=\mathrm{m}\left(\frac{\mathrm{m}}{\sqrt{\mathrm{m}^{2}+\mathrm{n}^{2}}}\right)+\mathrm{n}\left(\frac{\mathrm{n}}{\sqrt{\mathrm{m}^{2}+\mathrm{n}^{2}}}\right)$
$=\frac{\mathrm{m}^{2}+\mathrm{n}^{2}}{\sqrt{\mathrm{m}^{2}+\mathrm{n}^{2}}}$
=√(m2 + n2) = RHS
Hence Proved
Question 39
If $\cos
\alpha=\frac{12}{13}$ show that $\sin
\alpha(1-\tan \alpha)=\frac{35}{156}$
Sol :
We know that,
$\cos \theta=\frac{\text
{ side adjacent to angle } \theta}{\text { hypotenuse }}$
Or $\cos
\theta=\frac{\text { base }}{\text { Hypotenuse }}$
$\cos \alpha=\frac{12}{13} \Rightarrow
\frac{\mathrm{B}}{\mathrm{H}}=\frac{12}{13} \Rightarrow \frac{\mathrm{BC}}{\mathrm{AC}}=\frac{12}{13}$
Let,
Base =BC =
12k
Hypotenuse =AC = 13k
Where, k ia any positive
integer
So, by Pythagoras theorem, we can find the third side of a
triangle
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (AB)2 + (12k)2 = (13k)2
⇒ (AB)2 + 144k2 =
169k2
⇒ (AB)2 = 169
k2 –144 k2
⇒ (AB)2 = 25 k2
⇒ AB =√25 k2
⇒ AB =±5k
But side AB can’t be negative. So, AB = 5k
Now, we have to find sin α and tan α
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse }}$
Or $\cos \theta=\frac{\text { base }}{\text { Hypotenuse }}$
$\cos \alpha=\frac{12}{13} \Rightarrow \frac{\mathrm{B}}{\mathrm{H}}=\frac{12}{13} \Rightarrow \frac{\mathrm{BC}}{\mathrm{AC}}=\frac{12}{13}$
Base =BC = 12k
Hypotenuse =AC = 13k
Where, k ia any positive integer
So, by Pythagoras theorem, we can find the third side of a triangle
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (AB)2 + (12k)2 = (13k)2
⇒ (AB)2 + 144k2 = 169k2
⇒ (AB)2 = 169 k2 –144 k2
⇒ (AB)2 = 25 k2
⇒ AB =√25 k2
⇒ AB =±5k
But side AB can’t be negative. So, AB = 5k
Now, we have to find sin α and tan α
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse
}}$
Side opposite to angle α = AB
=5k
And Hypotenuse = AC
=13k
So, $\sin \alpha=\frac{5 \mathrm{k}}{13 \mathrm{k}}=\frac{5}{13}$
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to
angle } \theta}$
Side opposite to angle α = AB =5k
Side adjacent to angle α = BC =12k
So, $\tan \alpha=\frac{5 \mathrm{k}}{12 \mathrm{k}}=\frac{5}{12}$
Now, LHS = sin α (1 – tan α)
$=\frac{5}{13}\left(1-\frac{5}{12}\right)$
$=\frac{5}{13}\left(\frac{12-5}{12}\right)$
$=\frac{35}{156}$ =
RHS
Hence Proved
Question 40
If $\mathrm{q} \cos \theta=\sqrt{\mathrm{q}^{2}-\mathrm{p}^{2}}$,
prove that q sin θ = p.
Sol :
Given : q cos θ = √(q2 – p2)
$\Rightarrow \cos
\theta=\frac{\sqrt{\mathrm{q}^{2}-\mathrm{p}^{2}}}{\mathrm{q}}$
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse
}}$
Or $\cos \theta=\frac{\text { base }}{\text { Hypotenuse }}$
$\cos
\theta=\frac{\sqrt{\mathrm{q}^{2}-\mathrm{p}^{2}}}{\mathrm{q}} \Rightarrow
\frac{\mathrm{B}}{\mathrm{H}}=\frac{\sqrt{\mathrm{q}^{2}-\mathrm{p}^{2}}}{\mathrm{q}} \Rightarrow
\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{\sqrt{\mathrm{q}^{2}-\mathrm{p}^{2}}}{\mathrm{q}}$
Let,
Base =BC = √(q2 – p2)
Hypotenuse =AC = q
Where, k ia any positive integer
So, by Pythagoras theorem, we can find the third side of a
triangle
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (AB)2 + (√(q2 – p2))2 = (q)2
⇒ (AB)2 + (q2 – p2) = q2
⇒ (AB)2 =
q2 – q2 + p2)
⇒ (AB)2 = p2
⇒ AB =√p2
⇒ AB =±p
But
side AB can’t be negative. So, AB = p
Now, we have to find sin θ
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse
}}$
The side opposite to angle θ = AB
=p
And Hypotenuse = AC
=q
So, $\sin
\theta=\left(\frac{p}{q}\right)$
Now, LHS = q sin θ
$=\mathrm{q}\left(\frac{\mathrm{p}}{\mathrm{q}}\right)$
= q = RHS
Hence Proved
Question 41
If $\sin \theta=\frac{3}{5}$, show that : $\frac{\cos \theta-\frac{1}{\tan \theta}}{2 \cot
\theta}=-\frac{1}{5}$ Sol :
Given: $\sin \theta=\frac{3}{5}$
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse
}}$
Or $\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$\sin \theta=\frac{3}{5} \Rightarrow
\frac{\mathrm{P}}{\mathrm{H}}=\frac{3}{5} \Rightarrow \frac{\mathrm{AB}}{\mathrm{AC}}=\frac{3}{5}$
Let,
Perpendicular =AB =3k
and Hypotenuse =AC =5k
where, k is any positive
integer
So, by Pythagoras
theorem, we can find the third side of a triangle
In right angled ∆ ABC, we have
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (3k)2 +
(BC)2 = (5k)2
⇒ 9k2 + (BC)2 = 25k2
⇒ (BC)2 = 25
k2 –9k2
⇒ (BC)2 = 16k2
⇒ BC =√16k2
⇒ BC =±4k
But side BC can’t be negative. So, BC = 4k
Now, we have to find the value of cos θ and tan θ
We know that,
$\cos \theta=\frac{\text { base }}{\text { hypotenuse }}$
The side adjacent to angle θ or base = BC =4k
Hypotenuse = AC =5k
So, $\cos \theta=\frac{4 k}{5 k}=\frac{4}{5}$
Now,
We know that,
$\tan \theta=\frac{\text { perpendicular }}{\text {
base }}$
Perpendicular = AB
=3k
Base = BC =4k
So, $\tan \theta=\frac{3 \mathrm{k}}{4 \mathrm{k}}=\frac{3}{4}$
$\cot \theta=\frac{1}{\tan
\theta}=\frac{1}{\frac{3}{4}}=\frac{4}{3}$
Now, LHS $=\frac{\cos \theta-\frac{1}{\tan
\theta}}{2 \cot \theta}$
$=\frac{\left(\frac{4}{5}\right)-\left(\frac{1}{\frac{3}{4}}\right)}{2\left(\frac{4}{3}\right)}$
$=\frac{\left(\frac{4}{5}\right)-\left(\frac{4}{3}\right)}{\left(\frac{8}{3}\right)}$
$=\frac{\frac{12-20}{15}}{\left(\frac{8}{3}\right)}$
$=\frac{\left(-\frac{8}{15}\right)}{\left(\frac{8}{3}\right)}$
$=-\frac{1}{5}$ = RHS
Hence Proved
Question 42 A
Find the value
ofcos A sin B + sin A. cos B, if sin A= 4/5 and cos B = 12/13.
Sol :
Given: $\sin
A=\frac{4}{5}$ and $\cos B=\frac{12}{13}$
To find: cos A sin B + sin A cos B
As, we have the value of sin A and cos B but we don’t have the value of cos A and sin
B
So, First we find the value
of cos A and sin B
$\sin
A=\frac{4}{5}$
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse
}}$
Or $\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$\sin A=\frac{4}{5} \Rightarrow \frac{P}{H}=\frac{4}{5}$
Let,
Side opposite to angle A = 4k
and Hypotenuse = 5k
where, k is any positive
integer
So, by Pythagoras
theorem, we can find the third side of a triangle
⇒ (P)2 + (B)2 = (H)2
⇒ (4k)2 +
(B)2 = (5)2
⇒ 16 k2 + (B)2 = 25 k2
⇒ (B)2 = 25
k2 –16 k2
⇒ (B)2 = 9 k2
⇒ B =√9 k2
⇒ B =±3k [taking positive square root since, side cannot be negative]
So, Base = 3k
Now, we have to find the value of cos
A
We know that,
$\cos \theta=\frac{\text { side adjacent to angle }
\theta}{\text { hypotenuse }}$
Side adjacent to angle A =3k
Hypotenuse =5k
So, $\cos \mathrm{A}=\frac{3 \mathrm{k}}{5
\mathrm{k}}=\frac{3}{5}$
Now,
we have to find the sin B
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse
}}$
$\cos \mathbf{B}=\frac{12}{13}
\Rightarrow \frac{B}{H}=\frac{12}{13}$
Let,
Side adjacent to angle B =12k
Hypotenuse =13k
where, k is any positive integer
So, by Pythagoras theorem, we can find the third side of a
triangle
⇒ (B)2 +
(P)2 = (H)2
⇒ (12k)2 + (P)2 = (13)2
⇒ 144 k2 +
(P)2 = 169 k2
⇒ (P)2 = 169 k2 –144 k2
⇒ (P)2 = 25
k2
⇒ P =√25 k2
⇒ P =±5k [taking positive square root
since, side cannot be negative]
So, Perpendicular = 5k
Now, we have to find the value of sin B
We know that,
$\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$\sin \mathrm{B}=\frac{\mathrm{P}}{\mathrm{H}}=\frac{5
\mathrm{k}}{13 \mathrm{k}}=\frac{5}{13}$
Now, cos A sin B + sin A cos B
Putting the values of sin A, sin B cos A and Cos B, we get
$\Rightarrow\left(\frac{3}{5}\right)\left(\frac{5}{13}\right)+\left(\frac{4}{5}\right)\left(\frac{12}{13}\right)$
$\Rightarrow \frac{15+48}{5 \times 13}$
$\Rightarrow \frac{63}{65}$
Question 42 B
Find the value
ofsin A. cos B – cos A. sin B, if tan
A= √3 and sin B = 1/2.
Sol
:
Given: tan A =√3 and $\sin B=\frac{1}{2}$
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse
}}$
Or $\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$\sin \mathrm{B}=\frac{1}{2} \Rightarrow
\frac{\mathrm{P}}{\mathrm{H}}=\frac{1}{2}$
Let,
Side opposite to angle θ = 1k
and Hypotenuse = 2k
where, k is any positive integer
So, by Pythagoras theorem, we can find the third side of a
triangle
⇒ (AC)2 +
(BC)2 = (AB)2
⇒ (1k)2 + (BC)2 = (2k)2
⇒ k2 +
(BC)2 = 4k2
⇒ (BC)2 = 4k2 –k2
⇒ (BC)2 = 3
k2
⇒ BC =√3k2
⇒ BC =k√3
So, BC = k√3
Now, we have to find the value of cos B
We know that,
$\cos \theta=\frac{\text { side adjacent to angle }
\theta}{\text { hypotenuse }}$
The side adjacent to angle B = BC =k√3
Hypotenuse = AB =2k
So, $\cos \mathbf{B}=\frac{k \sqrt{3}}{2
k}=\frac{\sqrt{3}}{2}$
We know that,
$\tan \theta=\frac{\text { side opposite to angle } \theta}{\text { side adjacent to
angle } \theta}$
Or $\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
Given: tan A = √3
$\Rightarrow \tan
\mathrm{A}=\frac{\sqrt{3}}{1}$
$\tan
\mathrm{A}=\frac{\sqrt{3}}{1} \Rightarrow \frac{\mathrm{P}}{\mathrm{B}}=\frac{\sqrt{3}}{1} \Rightarrow
\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{\sqrt{3}}{1}$
Let,
The side opposite to angle A =BC = √3k
The side adjacent to angle A =AB = 1k
where k is any positive integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras
theorem
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (1k)2 + (√3k)2 =
(AC)2
⇒ (AC)2 = 1
k2 +3 k2
⇒ (AC)2 = 4 k2
⇒ AC =√2 k2
⇒ AC =±2k
But side AC can’t be negative. So, AC = 2k
Now, we will find the sin A and cos A
$\sin \theta=\frac{\text { side opposite to angle }
\theta}{\text { hypotenuse }}$
Side opposite to angle A = BC = k√3
and Hypotenuse = AC = 2k
So, $\sin \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{\mathrm{k} \sqrt{3}}{2
\mathrm{k}}=\frac{\sqrt{3}}{2}$
Now, we know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse
}}$
The side adjacent to
angle A = AB =1k
Hypotenuse = AC =2k
So, $\cos
\mathrm{A}=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{1 \mathrm{k}}{2 \mathrm{k}}=\frac{1}{2}$
Now, sin A. cos B – cos A. sin
B
Putting the values of sin A, sin B cos A and Cos B, we get
$\Rightarrow\left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{3}}{2}\right)-\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)$
$\Rightarrow \frac{3}{4}-\frac{1}{4}$
$\Rightarrow \frac{2}{4}$
$=\frac{1}{2}$
Question 42 C
Find the value
ofsin A. cos B + cos A. sin B.
if $\tan \mathrm{A}=\frac{1}{\sqrt{3}}$and tan B = √3.
Sol :
Given:
$\tan \mathrm{A}=\frac{1}{\sqrt{3}}$
$\tan \mathrm{A}=\frac{1}{\sqrt{3}} \Rightarrow
\frac{\mathrm{P}}{\mathrm{B}}=\frac{1}{\sqrt{3}}$
Let,
Side opposite to angle A =BC = 1k
Side adjacent to angle A =AB = k√3
where, k is any positive integer
Firstly we have to find the value of BC.
So, we can find the value of AC with the help of Pythagoras
theorem
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (√3k)2 + (1k)2 = (AC)2
⇒ (AC)2 = 1
k2 +3 k2
⇒ (AC)2 = 4 k2
⇒ AC =√2 k2
⇒ AC =±2k
But side AC can’t be negative. So, AC = 2k
Now, we will find the sin A and cos A
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse
}}$
Side opposite to
angle A = BC =
k
and Hypotenuse = AC =
2k
So, $\operatorname{Sin} \mathbf{A}=\frac{B C}{A C}=\frac{1 k}{2
k}=\frac{1}{2}$
Now, we know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse
}}$
Side adjacent to
angle A = AB =k√3
Hypotenuse = AC =2k
So, $\cos \mathbf{A}=\frac{A B}{B C}=\frac{k
\sqrt{3}}{2 k}=\frac{\sqrt{3}}{2}$
Now,
Given: tan B = √3
$\Rightarrow \tan \mathrm{B}=\frac{\sqrt{3}}{1}$
$\tan \mathrm{B}=\frac{\sqrt{3}}{1} \Rightarrow
\frac{\mathrm{P}}{\mathrm{B}}=\frac{\sqrt{3}}{1} \Rightarrow
\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\sqrt{3}}{1}$
Let,
Side opposite to angle B =AC = √3k
Side adjacent to angle B =AB = 1k
where, k is any positive integer
Firstly we have to find the value of BC.
So, we can find the value of AC with the help of Pythagoras
theorem
⇒ (AB)2 +
(AC)2 = (BC)2
⇒ (1k)2 + (√3k)2 =
(BC)2
⇒ (BC)2 = 1
k2 +3 k2
⇒ (BC)2 = 4 k2
⇒ BC =√2 k2
⇒ BC =±2k
But side BC can’t be negative. So, BC = 2k
Now, we will find the sin B and cos B
$\sin \theta=\frac{\text { side opposite to angle }
\theta}{\text { hypotenuse }}$
Side opposite to angle B = AC = k√3
and Hypotenuse = BC = 2k
So, $\sin \mathrm{B}=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{k} \sqrt{3}}{2
\mathrm{k}}=\frac{\sqrt{3}}{2}$
Now, we know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse
}}$
Side adjacent to
angle B = AB =1k
Hypotenuse = BC =2k
So, $\cos \mathbf{B}=\frac{A B}{B C}=\frac{1
k}{2 k}=\frac{1}{2}$
Now, sin A. cos B + cos A. sin B
Putting the values of sin A, sin B cos A and Cos B, we get
$\Rightarrow\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)+\left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{3}}{2}\right)$
$\Rightarrow \frac{1}{4}+\frac{3}{4}$
$\Rightarrow \frac{4}{4}$
=1
Question 42 D
Find the value
of$\frac{\tan A+\tan B}{1-\tan A \cdot \tan B}$, if sin A = $\frac{1}{\sqrt{2}}$and cos $\mathrm{B}=\frac{\sqrt{3}}{2}$
Sol :
Given $: \sin \mathrm{A}=\frac{1}{\sqrt{2}}$ and $\cos
\mathrm{B}=\frac{\sqrt{3}}{2}$
$\sin
\mathrm{A}=\frac{1}{\sqrt{2}}$
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse
}}$
Or $\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$\sin \mathrm{A}=\frac{1}{\sqrt{2}} \Rightarrow
\frac{\mathrm{P}}{\mathrm{H}}=\frac{1}{\sqrt{2}}$
Let,
Side opposite to angle A = k
and Hypotenuse = k√2
where, k is any positive integer
So, by Pythagoras theorem, we can find the third side of a
triangle
⇒ (P)2 +
(B)2 = (H)2
⇒ (k)2 + (B)2 = (k√2)2
⇒ k2 +
(B)2 = 2k2
⇒ (B)2 = 2k2 – k2
⇒ (B)2 =
k2
⇒ B =√k2
⇒ B =±k [taking positive square
root since, side cannot be negative]
So, Base = k
Now, we have to find the value of tan A
We know that,
$\tan \theta=\frac{\text { perpendicular }}{\text { base }}$
So, $\tan \mathrm{A}=\frac{\mathrm{k}}{\mathrm{k}}=1$
Now, we have to find the tan
B
We know that,
$\cos \theta=\frac{\text { side adjacent to angle }
\theta}{\text { hypotenuse }}$
$\cos
\mathbf{B}=\frac{\sqrt{3}}{2} \Rightarrow \frac{B}{H}=\frac{\sqrt{3}}{2}$
Let,
Side adjacent to angle B =k√3
Hypotenuse =2k
where, k is any positive
integer
So, by Pythagoras
theorem, we can find the third side of a triangle
⇒ (B)2 + (P)2 = (H)2
⇒ (k√3)2 +
(P)2 = (2k)2
⇒ 3k2 + (P)2 = 4k2
⇒ (P)2 =
4k2 –3 k2
⇒ (P)2 = k2
⇒ P =√k2
⇒ P =±k [taking positive square root since, side cannot be negative]
So, Perpendicular = k
Now, we have to find the value of sin
B
We know that,
$\tan \theta=\frac{\text { perpendicular }}{\text {
base }}$
So, $\tan \mathrm{B}=\frac{\mathrm{k}}{\mathrm{k}
\sqrt{3}}=\frac{1}{\sqrt{3}}$
Now, $\frac{\tan A+\tan
B}{1-\tan A \tan B}$
$\Rightarrow
\frac{(1)+\left(\frac{1}{\sqrt{3}}\right)}{1-(1)\left(\frac{1}{\sqrt{3}}\right)}$
$\Rightarrow \frac{\frac{\sqrt{3}+1}{\sqrt{3}}}{\frac{\sqrt{3}-1}{\sqrt{3}}}$
$\Rightarrow \frac{\sqrt{3}+1}{\sqrt{3}-1}$
Now, multiply and divide by the conjugate of √3 – 1, we get
$\Rightarrow \frac{\sqrt{3}+1}{\sqrt{3}-1} \times
\frac{\sqrt{3}+1}{\sqrt{3}+1}$
$\Rightarrow
\frac{(\sqrt{3}+1)^{2}}{(\sqrt{3})^{2}-(1)^{2}}$ [∵ (a – b)(a+b) =
(a2 – b2)]
$\Rightarrow \frac{3+1+2 \sqrt{3}}{3-1}$
$\Rightarrow \frac{4+2 \sqrt{3}}{2}$
⇒ 2+√3
Question 42 E
Find the value
ofsec A. tan A+tan2A – cosec A, if tan A =2
Sol :
Given: tan A = 2 ⇒ tan2A = 4
We know that, sec2 A = 1+ tan2A
⇒ sec2 A = 1 +
4
⇒ sec2 A =
5
⇒ sec A =√5
$\Rightarrow \cos A=\frac{1}{\sqrt{5}}$
Now, we know that tan A$=\frac{\sin A}{\cos A}$
$\Rightarrow 2=\frac{\sin
A}{\frac{1}{\sqrt{5}}}$
⇒ 2 =√5 sin A
$\Rightarrow \sin A=\frac{2}{\sqrt{5}}$
$\Rightarrow \operatorname{cosec} A=\frac{\sqrt{5}}{2}$
Now, putting all the values in the given equation, we get
sec A. tan A+tan2A – cosec
A
$\Rightarrow(\sqrt{5})(2)+(4)-\left(\frac{\sqrt{5}}{2}\right)$
$\Rightarrow \frac{4 \sqrt{5}+8-\sqrt{5}}{2}$
$\Rightarrow \frac{3 \sqrt{5}+8}{2}$
Question 42 F
Find the value
of$\frac{1}{\tan \mathrm{A}}+\frac{\sin \mathrm{A}}{1+\cos \mathrm{A}}$, if
cosec A = 2
Sol :
Given: cosec A =2
Now, we have to find $\frac{1}{\tan A}+\frac{\sin A}{1+\cos A}$
First, we simplify the above given
trigonometry equation, we get
$\frac{1}{\frac{\sin A}{\cos A}}+\frac{\sin A}{1+\cos A}$
$\Rightarrow \frac{\cos A}{\sin A}+\frac{\sin
A}{1+\cos A}$
Taking the LCM, we get
$\Rightarrow \frac{\cos A(1+\cos A)+\sin A(\sin A)}{(\sin A)(1+\cos A)}$
$\Rightarrow \frac{\cos A+\cos ^{2} A+\sin ^{2}
A}{\sin A(1+\cos A)}$ [∵ cos2θ +sin2 θ = 1]
$\Rightarrow \frac{\cos A+1}{\sin A(1+\cos
A)}$
$\Rightarrow \frac{1}{\sin
A}$ [∵ cosec θ $=\frac{1}{\sin \theta}$ ]
⇒ cosec A
⇒ 2
Question 43 A
If $\sin \mathrm{B}=\frac{1}{2}$, prove that : 3 cos B –
4cos3 B = 0
Sol :
Given: $\sin B=\frac{1}{2}$
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse
}}$
Or $\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$\sin B=\frac{1}{2} \Rightarrow
\frac{P}{H}=\frac{1}{2} \Rightarrow \frac{A B}{A C}=\frac{1}{2}$
Let,
Perpendicular =AB =k
and Hypotenuse =AC =2k
where, k is any positive integer
So, by Pythagoras theorem, we can find the third side of a
triangle
In right
angled ∆ ABC, we have
⇒ (AB)2 + (BC)2 = (AC)2
⇒ (k)2 +
(BC)2 = (2k)2
⇒ k2 + (BC)2 = 4k2
⇒ (BC)2 =
4k2 –k2
⇒ (BC)2 = 3k2
⇒ BC =√3k2
⇒ BC =k√3
So,
BC = k√3
Now, we have to find
the value of cos B
We know that,
$\cos \theta=\frac{\text { base }}{\text { hypotenuse }}$
Side adjacent to angle B or base = BC = k√3
Hypotenuse = AC =2k
So, $\cos \mathrm{B}=\frac{\mathrm{k} \sqrt{3}}{2
\mathrm{k}}=\frac{\sqrt{3}}{2}$
Now, LHS = 3 cos B – 4cos3 B
$\Rightarrow 3\left(\frac{\sqrt{3}}{2}\right)-4\left(\frac{\sqrt{3}}{2}\right)^{3}$
$\Rightarrow \frac{3 \sqrt{3}}{2}-4\left(\frac{3 \sqrt{3}}{8}\right)$
$\Rightarrow \frac{3 \sqrt{3}}{2}-\frac{3 \sqrt{3}}{2}=0$
=RHS
Hence Proved
Question 43 B
If $\cos \theta=\frac{\sqrt{3}}{2}$, prove that: 3sinθ –
4sin3θ = 1.
Sol :
We know that,
$\cos \theta=\frac{\text { Base }}{\text { hypotenuse }}$
$\cos \theta=\frac{\sqrt{3}}{2} \Rightarrow
\frac{\mathrm{B}}{\mathrm{H}}=\frac{\sqrt{3}}{2}$
Let AB =k√3 and BC = 2k
In right angled ∆ABC, we have
B2 + P2 = H2
⇒ (k√3)2 +
P2 = (2k)2
⇒ P2 + 3k2 = 4k2
⇒ P2 =
4k2 – 3k2
⇒ P2 = k2
⇒ P =√k2
⇒ P = ±k
⇒ P = k [taking positive square
root since, side cannot be negative]
Now,
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse
}}$
Or $\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$\therefore \sin \theta=\frac{P}{H}=\frac{k}{2
k}=\frac{1}{2}$
Now, LHS = 3sin θ – 4sin3 θ
$=3\left(\frac{1}{2}\right)-4\left(\frac{1}{2}\right)^{3}$
$\Rightarrow \frac{3}{2}-\frac{4}{8}$
$\Rightarrow \frac{3}{2}-\frac{1}{2}$
$\Rightarrow \frac{3-1}{2}$
$\Rightarrow \frac{2}{2}$
⇒ 1 = RHS
Hence Proved
Question 43 C
If $\sec \theta=\frac{5}{4}$, prove that : $\frac{\tan \theta}{1+\tan ^{2}
\theta}=\frac{\sin \theta}{\sec \theta}$
Sol :
Given: $\sec \theta=\frac{5}{4}$
We know that,
$\sec \theta=\frac{\text { hypotenuse }}{\text { base }}$
$\operatorname{Sec} \theta=\frac{5}{4} \Rightarrow
\frac{\mathrm{H}}{\mathrm{B}}=\frac{5}{4} \Rightarrow \frac{\mathrm{AC}}{\mathrm{BC}}=\frac{5}{4}$
Let,
BC = 4k and AC = 5k
where, k is any positive
integer.
In right
angled ∆ABC, we
have
(AB)2 +
(BC)2 = (AC)2 [by using Pythagoras theorem]
⇒ (AB)2 +
(4k)2 = (5k )2
⇒ (AB)2 + 16k2 = 25k2
⇒ (AB)2 =
25k2 – 16k2
⇒ (AB)2 = 9k2
⇒ AB = √9k2
⇒ AB =±3k [taking positive square root
since, side cannot be negative]
Now, we have to find the value of other trigonometric ratios.
We, know that
$\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$=\frac{A B}{A C}=\frac{3 k}{5 k}=\frac{3}{5}$
$\cos \theta=\frac{\text { Base }}{\text { Hypotenuse }}$
$=\frac{B C}{A C}=\frac{4 k}{5 k}=\frac{4}{5}$
$\tan \theta=\frac{\text { Perpendicular }}{\text { Base }}$
$=\frac{A B}{B C}=\frac{3 k}{4 k}=\frac{3}{4}$
Now, LHS $=\frac{\tan
\theta}{1+\tan ^{2} \theta}$
$=\frac{\left(\frac{3}{4}\right)}{1+\left(\frac{3}{4}\right)^{2}}$
$=\frac{\left(\frac{3}{4}\right)}{1+\left(\frac{9}{16}\right)}$
$=\frac{\left(\frac{3}{4}\right)}{\left(\frac{16+9}{16}\right)}$
$=\frac{\left(\frac{3}{4}\right)}{\left(\frac{25}{16}\right)}$
$=\frac{3}{4} \times \frac{16}{25}$
$=\frac{12}{25}$
Now, RHS $=\frac{\sin \theta}{\sec \theta}$
$=\frac{\left(\frac{3}{5}\right)}{\left(\frac{5}{4}\right)}$
$=\frac{3}{5} \times \frac{4}{5}$
$=\frac{12}{25}$
∴ LHS = RHS
Hence Proved
Question 43 D
$\cot B=\frac{12}{5}$
, prove that : tan2B – sin2 B=sin4 B
sec2 B.
Sol :
We know that,
$\cot \theta=\frac{\text { side adjacent to angle } \theta}{\text { side opposite to
angle } \theta}$
Or $\cot \theta=\frac{\text { base }}{\text { perpendicular }}$
$\cot B=\frac{12}{5} \Rightarrow
\frac{B}{P}=\frac{12}{5} \Rightarrow \frac{A B}{B C}=\frac{12}{5}$
Let,
Side adjacent to angle B =AB = 12k
Side opposite to angle B =BC = 5k
where, k is any positive integer
Firstly we have to find the value of AC.
So, we can find the value of AC with the help of Pythagoras
theorem
⇒ (AB)2 +
(BC)2 = (AC)2
⇒ (12k)2 + (5k)2 = (AC)2
⇒ (AC)2 = 144
k2 +25 k2
⇒ (AC)2 = 169 k2
⇒ AC =√169 k2
⇒ AC =±13k
But side AC can’t be negative. So, AC = 13k
Now, we will find the sin θ
$\sin \theta=\frac{\text { side opposite to angle }
\theta}{\text { hypotenuse }}$
Side opposite to angle B = BC = 5k
and Hypotenuse = AC = 13k
So, $\sin
\mathrm{B}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{5 \mathrm{k}}{13 \mathrm{k}}=\frac{5}{13}$
Now, we know that,
$\cos \theta=\frac{\text { side adjacent to angle }
\theta}{\text { hypotenuse }}$
Side adjacent to angle B = AB =12k
Hypotenuse = AC =13k
So, $\cos
\mathrm{B}=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{12 \mathrm{k}}{13 \mathrm{k}}=\frac{12}{13}$
$\tan
\mathrm{B}=\frac{\mathrm{P}}{\mathrm{B}}=\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{5}{12}$
$\sec \mathrm{B}=\frac{1}{\cos
\mathrm{B}}=\frac{1}{\frac{12}{13}}=\frac{13}{12}$
Now, LHS = tan2B – sin2 B
$=\left(\frac{5}{12}\right)^{2}-\left(\frac{5}{13}\right)^{2}$
$=\frac{25}{144}-\frac{25}{169}$
$=\frac{4225-3600}{144 \times 169}$
$=\frac{625}{144 \times 169}$
$=\frac{625}{24336}$
Now, RHS = sin4 B sec2 B
$=\left(\frac{5}{13}\right)^{4}\left(\frac{13}{12}\right)^{2}$
$=\left(\frac{5}{13}\right)^{2}\left(\frac{5}{13}\right)^{2}\left(\frac{13}{12}\right)^{2}$
$=\frac{625}{144 \times 169}$
$=\frac{625}{24336}$
Now, LHS = RHS
Hence Proved
Question 44
If $\cos \theta=\frac{\mathrm{q}}{\sqrt{\mathrm{p}^{2}+\mathrm{q}^{2}}}$, prove that
$\left(\frac{\sqrt{\mathrm{p}^{2}+\mathrm{q}^{2}}}{\mathrm{p}}+\frac{\mathrm{q}}{\mathrm{p}}\right)^{2}=
\frac{\sqrt{\mathrm{p}^{2}+\mathrm{q}^{2}}+\mathrm{q}}{\sqrt{\mathrm{p}^{2}+\mathrm{q}^{2}-\mathrm{q}}}$ Sol :
Given: $\cos
\theta=\frac{q}{\sqrt{p^{2}+q^{2}}}$
Now, squaring both the sides, we get
$=\cos ^{2} \theta=\frac{\mathrm{q}^{2}}{\mathrm{p}^{2}+\mathrm{q}^{2}}$
$\Rightarrow \mathrm{p}^{2}+\mathrm{q}^{2}=\frac{\mathrm{q}^{2}}{\cos ^{2} \theta}$
$\Rightarrow \mathrm{p}^{2}=\frac{\mathrm{q}^{2}}{\cos ^{2} \theta}-\mathrm{q}^{2}$
$\Rightarrow \mathrm{p}^{2}=\frac{\mathrm{q}^{2}-\mathrm{q}^{2} \cos ^{2} \theta}{\cos ^{2} \theta}$
$\Rightarrow \mathrm{p}^{2}=\frac{\mathrm{q}^{2}\left(1-\cos ^{2} \theta\right)}{\cos ^{2} \theta}$
$\Rightarrow \mathrm{p}^{2}=\frac{\mathrm{q}^{2} \sin ^{2} \theta}{\cos ^{2} \theta}$
⇒ p2 = q2 tan2θ
…(1)
Now, solving
LHS $=\left(\frac{\sqrt{\mathrm{p}^{2}+\mathrm{q}^{2}}}{\mathrm{p}}+\frac{\mathrm{q}}{\mathrm{p}}\right)^{2}$
Putting the value of
p2 in the above equation, we get
$=\left(\frac{\sqrt{q^{2} \tan ^{2} \theta+q^{2}}}{p}+\frac{q}{p}\right)^{2}$
$\Rightarrow\left(\frac{\sqrt{q^{2}\left(\tan ^{2} \theta+1\right)}}{p}+\frac{q}{p}\right)^{2}$
$\Rightarrow\left(\frac{\sqrt{\mathrm{q}^{2} \sec ^{2}
\theta}}{\mathrm{p}}+\frac{\mathrm{q}}{\mathrm{p}}\right)^{2}$ [∵ 1+ tan2 θ = sec2 θ]
$\Rightarrow\left(\frac{\mathrm{q} \sec \theta}{\mathrm{p}}+\frac{\mathrm{q}}{\mathrm{p}}\right)^{2}$
$\Rightarrow \frac{\mathrm{q}^{2}(\sec \theta+1)^{2}}{\mathrm{p}^{2}}$
$\Rightarrow \frac{\mathrm{q}^{2}(\sec \theta+1)^{2}}{\mathrm{q}^{2} \tan ^{2}
\theta}$ (from Eq. (1))
$\Rightarrow \frac{(\sec \theta+1)^{2}}{\left(\sec ^{2}
\theta-1\right)}$
$\Rightarrow \frac{(\sec \theta+1)(\sec \theta+1)}{(\sec \theta-1)(\sec \theta+1)}$ [∵(a + b) (a – b) = (a2 – b2)]
$\Rightarrow \frac{\sec \theta+1}{\sec \theta-1}$
Now, we solve the RHS
$=\frac{\sqrt{\mathrm{p}^{2}+\mathrm{q}^{2}}+\mathrm{q}}{\sqrt{\mathrm{p}^{2}+\mathrm{q}^{2}}-\mathrm{q}}$
$=\frac{\sqrt{\mathrm{q}^{2} \tan ^{2} \theta+\mathrm{q}^{2}}+\mathrm{q}}{\sqrt{\mathrm{q}^{2} \tan ^{2} \theta+\mathrm{q}^{2}}-\mathrm{q}}$
$=\frac{\sqrt{\mathrm{q}^{2}\left(\tan ^{2} \theta+1\right)}+\mathrm{q}}{\sqrt{\mathrm{q}^{2}\left(\tan ^{2} \theta+1\right)}-\mathrm{q}}$
$=\frac{\sqrt{\mathrm{q}^{2} \sec ^{2}}+\mathrm{q}}{\sqrt{\mathrm{q}^{2} \sec ^{2}
\theta}-\mathrm{q}}$ [∵ 1+ tan2 θ = sec2 θ]
$=\frac{\operatorname{qsec} \theta+q}{\operatorname{qsec} \theta-q}$
$\Rightarrow \frac{\sec \theta+1}{\sec \theta-1}$
∴ LHS = RHS
Hence Proved
Question
45
In the given figure,
BC = 15 cm and sin B = 4/5, show that $\tan ^{2} \mathrm{B}-\frac{1}{\cos ^{2}
\mathrm{B}}=-1$
Sol :
Given:
BC =15cm and $\sin B=\frac{4}{5}$
We know that,
$\sin \theta=\frac{\text { side opposite to angle } \theta}{\text { hypotenuse
}}$
Or $\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}$
$\sin \mathrm{B}=\frac{4}{5} \Rightarrow
\frac{\mathrm{P}}{\mathrm{H}}=\frac{4}{5} \Rightarrow \frac{\mathrm{AC}}{\mathrm{AB}}=\frac{4}{5}$
Let,
Side opposite to angle
B = 4k
and Hypotenuse = 5k
where, k is any positive
integer
So, by Pythagoras
theorem, we can find the third side of a triangle
⇒ (AC)2 + (BC)2 = (AB)2
⇒ (4k)2 +
(BC)2 = (5)2
⇒ 16k2 + (BC)2 = 25k2
⇒ (BC)2 = 25
k2 –16 k2
⇒ (BC)2 = 9 k2
⇒ BC =√9 k2
⇒ BC =±3k
But side BC can’t be negative. So, BC = 3k
Now, we have to find the value of cos B and tan B
We know that,
$\cos \theta=\frac{\text { side adjacent to angle } \theta}{\text { hypotenuse
}}$
Side adjacent to
angle B = BC =3k
Hypotenuse = AB =5k
So, $\cos B=\frac{3 k}{5
k}=\frac{3}{5}$
Now, tan
B
We know that,
$\tan \theta=\frac{\text { side opposite to angle }
\theta}{\text { side adjacent to angle } \theta}$
side opposite to angle B = AC =4k
Side adjacent to angle B = BC =3k
So, $\tan \mathrm{B}=\frac{4 \mathrm{k}}{3 \mathrm{k}}=\frac{4}{3}$
Now, $\tan ^{2}
\mathrm{B}-\frac{1}{\cos ^{2} \mathrm{B}}$
$=\left(\frac{4}{3}\right)^{2}-\left(\frac{1}{\frac{3}{5}}\right)^{2}$
$=\frac{16}{9}-\frac{25}{9}$
$=\frac{-9}{9}$
= –1 = RHS
Hence Proved
Question 46
In the given figure,
find 3 tan θ – 2 sin α + 4 cos α.
Sol :
First
of all, we find the value of RS
In right angled ∆RQS, we have
(RQ)2 + (QS)2 = (RS)2
⇒ (8)2 +
(6)2 = (RS)2
⇒ 64 + 36 = (RS)2
⇒ RS =√100
⇒ RS =±10 [taking positive square root, since side cannot be negative]
⇒ RS =10
$\therefore \sin \alpha=\frac{P}{H}=\frac{8}{10}=\frac{4}{5}$
$\cos \alpha=\frac{B}{H}=\frac{6}{10}=\frac{3}{5}$
Now, we find the value of QP
In right angled ∆RQP
(RQ)2 +
(QP)2 = (RP)2
⇒ (8)2 + (QP)2 = (17)2
⇒ 64 + (QP)2 = 289
⇒ (QP)2 =289–64
⇒ (QP)2 =225
⇒ QP =√225
⇒ QP =±15 [taking positive square root, since side cannot be negative]
⇒ QP =15
tan
θ$=\frac{\mathrm{P}}{\mathrm{B}}=\frac{8}{15}$
Now, 3 tan θ – 2 sinα + 4cos α
⇒ $3\left(\frac{8}{15}\right)-2\left(\frac{4}{5}\right)+4\left(\frac{3}{5}\right)$
⇒ $\frac{24}{15}-\frac{8}{5}+\frac{12}{5}$
⇒ $\frac{24-24+36}{15}$
⇒$\frac{36}{15}$
⇒$\frac{12}{5}$
Question 47
In the given figure
ΔABC is right angled at B and BD is perpendicular to AC. Find (i) cos θ, (ii) cot α.
Sol :
Firstly, we find the value of
AC
In right angled ∆ABC
(AB)2 + (BC)2 =
(AC)2
⇒ (12)2 +
(5)2 = (AC)2
⇒ 144+25
=(AC)2
⇒ (AC)2 =169
⇒ AC =√169
⇒ AC =±13
⇒ AC =13 [taking positive
square root since, side cannot be negative]
(i) $\cos \theta=\frac{\text { Base
}}{\text { Hypotenuse }}=\frac{12}{13}$
(ii) $\cot \alpha=\frac{\text { Base
}}{\text { Perpendicular }}=\frac{12}{5}$
In right angled ∆ABC
(AB)2 + (BC)2 = (AC)2
⇒ (12)2 + (5)2 = (AC)2
⇒ 144+25 =(AC)2
⇒ (AC)2 =169
⇒ AC =√169
⇒ AC =±13
⇒ AC =13 [taking positive square root since, side cannot be negative]
(i) $\cos \theta=\frac{\text { Base }}{\text { Hypotenuse }}=\frac{12}{13}$
(ii) $\cot \alpha=\frac{\text { Base }}{\text { Perpendicular }}=\frac{12}{5}$
Question 48
If 5
sin2 θ + cos2 θ = 2, find the value of sin θ.
Sol :
Given: 5 sin2 θ + cos2 θ = 2
⇒ 5 sin2 θ + (1–
sin2 θ) = 2 [∵ sin2 θ +
cos2 θ = 1]
⇒ 5 sin2 θ + 1 – sin2 θ = 2
⇒ 4 sin2 θ = 2 –
1
⇒ 4 sin2 θ =
1
$\Rightarrow \quad \sin ^{2} \theta=\frac{1}{4}$
$\Rightarrow \quad \sin \theta=\sqrt{\frac{1}{4}}$
$\Rightarrow \quad \sin \theta=\pm \frac{1}{2}$
Question 49
If 7
sin2 θ + 3 cos2 θ =4, find the value of tan θ.
Sol :
Given : 7 sin2 θ + 3 cos2 θ =4
⇒ 7 sin2 θ +
3(1– sin2 θ) = 4 [∵ sin2 θ +
cos2 θ = 1]
⇒ 7 sin2 θ + 3 –3 sin2 θ = 4
⇒ 4 sin2 θ = 4 –
3
⇒ 4 sin2 θ =
1
$\Rightarrow \sin ^{2} \theta=\frac{1}{4}$
$\Rightarrow \sin \theta=\sqrt{\frac{1}{4}}$
$\Rightarrow \sin \theta=\pm \frac{1}{2}$
Put the value of $\sin
^{2} \theta=\frac{1}{4}$ in given equation, we
get
$\Rightarrow 7\left(\frac{1}{2}\right)^{2}+3 \cos ^{2} \theta=4$
$\Rightarrow \frac{7}{4}+3 \cos ^{2} \theta=4$
$\Rightarrow 3 \cos ^{2} \theta=4-\frac{7}{4}$
$\Rightarrow 3 \cos ^{2} \theta=\frac{16-7}{4}$
$\Rightarrow 3 \cos ^{2} \theta=\frac{9}{4}$
$\Rightarrow \cos ^{2} \theta=\frac{3}{4}$
$\Rightarrow \cos \theta=\sqrt{\frac{3}{4}}$
$\Rightarrow \cos \theta=\pm \frac{\sqrt{3}}{2}$
Now, we know that tan θ $=\frac{\sin \theta}{\cos \theta}$
$\Rightarrow \tan \theta=\frac{\left(\pm \frac{1}{2}\right)}{\left(\pm \frac{\sqrt{3}}{2}\right)}$
$\Rightarrow \tan \theta=\pm \frac{1}{\sqrt{3}}$
Question 50
If 4 cos θ + 3 sin θ =
5, find the value of tan θ.
Sol :
Given : 4 cos θ+ 3 sin θ =
5
Squaring both the sides, we get
⇒ (4 cos θ+ 3 sin θ)2 = 25
⇒ 16 cos2 θ + 9 sin2 θ + 2(4cos θ)(3sin θ)= 25
[∵ (a +
b)2 =a2 +b2 +2ab]
⇒ 16 cos2 θ + 9 sin2 θ + 24 cosθ sinθ =
25
Divide by
cos2 θ, we get
$\Rightarrow \frac{16 \cos ^{2}
\theta}{\cos ^{2} \theta}+\frac{9 \sin ^{2} \theta}{\cos ^{2} \theta}+\frac{24 \cos \theta \sin \theta}{\cos
^{2} \theta}=\frac{25}{\cos ^{2} \theta}$
⇒ 16 + 9tan2 θ + 24 tanθ = 25sec2 θ
⇒ 16 + 9tan2 θ + 24 tanθ = 25(1 + tan2 θ)
[∵ 1+ tan2θ =
sec2 θ]
⇒ 16 +
9tan2 θ + 24 tanθ = 25+ 25 tan2 θ
⇒ 16tan2 θ – 24tanθ + 9 = 0
⇒ 16tan2 θ – 12 tanθ – 12 tanθ +9 = 0
⇒ 4tanθ (4tan θ – 3) – 3(4tan θ – 3) = 0
⇒ (4tan θ – 3)2 = 0
$\Rightarrow \tan \theta=\frac{3}{4}$
Squaring both the sides, we get
⇒ (4 cos θ+ 3 sin θ)2 = 25
⇒ 16 cos2 θ + 9 sin2 θ + 2(4cos θ)(3sin θ)= 25 [∵ (a + b)2 =a2 +b2 +2ab]
⇒ 16 cos2 θ + 9 sin2 θ + 24 cosθ sinθ = 25
$\Rightarrow \frac{16 \cos ^{2} \theta}{\cos ^{2} \theta}+\frac{9 \sin ^{2} \theta}{\cos ^{2} \theta}+\frac{24 \cos \theta \sin \theta}{\cos ^{2} \theta}=\frac{25}{\cos ^{2} \theta}$
⇒ 16 + 9tan2 θ + 24 tanθ = 25sec2 θ
⇒ 16 + 9tan2 θ + 24 tanθ = 25(1 + tan2 θ) [∵ 1+ tan2θ = sec2 θ]
⇒ 16 + 9tan2 θ + 24 tanθ = 25+ 25 tan2 θ
⇒ 16tan2 θ – 24tanθ + 9 = 0
⇒ 16tan2 θ – 12 tanθ – 12 tanθ +9 = 0
⇒ 4tanθ (4tan θ – 3) – 3(4tan θ – 3) = 0
⇒ (4tan θ – 3)2 = 0
$\Rightarrow \tan \theta=\frac{3}{4}$
Question 51
If 7 sin A + 24 cos A
= 25, find the value of tan A.
Sol :
Given : 7 sin A + 24 cos A = 25
Squaring both the sides, we get
⇒ (7 sin A + 24 cos
A)2 = 625
⇒ 49 sin2 A +576 cos2 A + 2(7sin A) (24cos A) = 625
[∵ (a +
b)2 =a2 +b2 +2ab]
⇒ 49 sin2 A +576 cos2 A + 336 cosA sinA = 625
Divide by cos2 θ, we get
$\Rightarrow \frac{49 \sin ^{2} \mathrm{A}}{\cos ^{2}
\mathrm{A}}+\frac{576 \cos ^{2} \mathrm{A}}{\cos ^{2} \mathrm{A}}+\frac{336 \cos \mathrm{A} \sin \mathrm{A}}{\cos
^{2} \mathrm{A}}=\frac{625}{\cos ^{2} \mathrm{A}}$
⇒ 49tan2 A +576+ 336 tanA =
625sec2 A
⇒ 49tan2 A +576+ 336 tanA = 625(1 + tan2 A) [∵ 1+ tan2θ = sec2 θ]
⇒ 49tan2 A +576+
336 tanθA = 625+625 tan2 A
⇒ 576tan2 A – 336tanA + 49 = 0
⇒ 576tan2 A – 168 tanA – 168 tanA +49 = 0
⇒ 24tanθ (24tan A – 7) – 7(24tan A – 7) = 0
⇒ (24tan A – 7)2 = 0
$\Rightarrow \tan \mathrm{A}=\frac{7}{24}$
Question 52
If 9 sin θ + 40 cos θ=
41, find the value of cos θ and cosec θ
Sol :
Given: 9 sin θ + 40 cos θ= 41
⇒ 9sinθ = 41 – 40 cosθ …(i)
Squaring both sides, we get
⇒ 81sin2 θ = 1681+1600 cos2 θ – 2(41) (40cos θ)
[∵ (a –
b)2 =a2 +b2 –2ab]
⇒ 81 (1– cos2 θ) =1681+1600 cos2 θ – 3280cosθ
⇒ 81 – 81cos2 θ =
1681 +1600cos2 θ – 3280 cosθ
⇒ 1681cos2 θ –3280cos θ +1600 = 0
⇒ (41)2 cos2 θ – 2(41) (40cos θ) + (40)2 =
0
⇒ (41cos θ – 40 )2 =
0
$\Rightarrow \cos \theta=\frac{40}{41}$
Now, putting the value of cos θ in Eq.
(i), we get
$\Rightarrow 9 \sin \theta=41-40\left(\frac{40}{41}\right)$
$\Rightarrow 9 \sin \theta=\left(\frac{1681-1600}{41}\right)$
$\Rightarrow \sin \theta=\left(\frac{81}{41 \times 9}\right)$
$\Rightarrow \frac{1}{\operatorname{cosec} \theta}=\left(\frac{9}{41}\right)$
$\Rightarrow \operatorname{cosec} \theta=\frac{41}{9}$
Question 53
If tan A + sec A = 3,
find the value of sin A.
Sol :
tan A + sec A = 3
⇒ tanA = 3 – secA
Squaring both the sides, we get
⇒ tan2 A =(3 –
secA)2
⇒ tan2 A = 9 +
sec2A – 6sec A
⇒ sec2 A – 1 = 9 + sec2A – 6sec A [∵ 1+ tan2 A = sec2 A]
⇒ –1 – 9 = –6secA
⇒ – 10 = –6sec A
$\Rightarrow \sec A=\frac{10}{6}$
$\Rightarrow \frac{1}{\cos
A}=\frac{5}{3}\left[\because \sec A=\frac{1}{\cos A}\right]$
$\Rightarrow \cos A=\frac{3}{5}$
Now, tan A + sec A = 3
$\Rightarrow \frac{\sin A}{\cos A}+\frac{1}{\cos
A}=3\left[\because \tan A=\frac{\sin A}{\cos A}\right]$
$\Rightarrow \frac{\sin A}{\cos A}=\frac{3 \cos A-1}{\cos A}$
⇒ sin A = 3cosA – 1
$\Rightarrow \sin A=3\left(\frac{3}{5}\right)-1$
$\Rightarrow \sin A=\left(\frac{9-5}{5}\right)$
$\Rightarrow \sin A=\left(\frac{4}{5}\right)$
Question 54
If cosec A + cot A =
5, find the value of cos A.
Sol :
cosec A + cot A = 5
⇒ cotA = 5 – cosecA
Squaring both the sides, we get
⇒ cot2 A =(5 –
cosecA)2
⇒ cot2 A = 25 + cosec2A – 10cosec A
⇒ cosec2 A – 1 =
25 + cosec2A – 10cosec A [∵ 1+ cot2 A =
cosec2 A]
⇒ –1 – 25 = –10cosecA
⇒ – 26 = –10cosec A
$\Rightarrow \operatorname{cosec} A=\frac{26}{10}$
$\Rightarrow \frac{1}{\sin
A}=\frac{13}{5}\left[\because \operatorname{cosec} A=\frac{1}{\sin A}\right]$
$\Rightarrow \sin \mathrm{A}=\frac{5}{13}$
Now, cosec A + cot A = 5
$\Rightarrow \frac{1}{\sin A}+\frac{\cos A}{\sin A}=5\left[\because \cot A=\frac{\cos
A}{\sin A}\right]$
$\Rightarrow
\frac{13}{5}+\frac{\cos A}{\frac{5}{13}}=5$
$\Rightarrow \frac{13}{5}+\frac{13 \cos A}{5}=5$
$\Rightarrow \frac{13 \cos A}{5}=5-\frac{13}{5}$
$\Rightarrow \frac{13 \cos A}{5}=\frac{25-13}{5}$
$\Rightarrow \cos A=\frac{12}{13}$
Question 55
If tan θ + sec θ = x,
show that
$\sin \theta=\frac{x^{2}-1}{x^{2}+1}$
Sol :
tan θ+ sec θ = x
⇒ tan θ = x – sec θ
Squaring both sides, we get
⇒ tan2 θ =(x – secθ)2
⇒ tan2 θ =
x2 + sec2θ – 2xsec θ
⇒ sec2 θ – 1 = x2 + sec2θ – 2xsec θ
[∵ 1+ tan2 A = sec2 A]
⇒ –1 – x2 =
–2xsecθ
$\Rightarrow \sec
\theta=\frac{1+x^{2}}{2 x}$
Now,
tan θ = x – sec θ
$\Rightarrow \frac{\sin \theta}{\cos \theta}=x-\sec \theta$
$\Rightarrow \sin \theta\left(\frac{1+x^{2}}{2
x}\right)=x-\left(\frac{1+x^{2}}{2 x}\right)$
$\Rightarrow \sin \theta\left(\frac{1+\mathrm{x}^{2}}{2 \mathrm{x}}\right)=\left(\frac{2
\mathrm{x}^{2}-1+\mathrm{x}^{2}}{2 \mathrm{x}}\right)$
$\Rightarrow \sin \theta\left(\frac{1+x^{2}}{2 x}\right)=\left(\frac{x^{2}-1}{2
x}\right)$
$\Rightarrow \sin
\theta=\frac{x^{2}-1}{x^{2}+1}$ = RHS
Hence Proved
$\sin \theta=\frac{x^{2}-1}{x^{2}+1}$
Question 56
If cos θ +sin θ=1,
prove that cos θ – sin θ = ± 1
Sol :
Using the formula,
(a+b)2 + (a –
b)2 = 2(a2+b2)
⇒ (cos θ +sin
θ)2 + (cos θ – sin θ)2 = 2(cos2θ +
sin2 θ)
⇒ 1 + (cos θ – sin θ)2 =
2(1)
⇒ (cos θ – sin θ)2 = 2 –1
⇒ (cos θ – sin θ)2 = 1
⇒ (cos θ – sin θ)
=√1
⇒ (cos θ – sin θ) = ±1
(a+b)2 + (a – b)2 = 2(a2+b2)
⇒ (cos θ +sin θ)2 + (cos θ – sin θ)2 = 2(cos2θ + sin2 θ)
⇒ 1 + (cos θ – sin θ)2 = 2(1)
⇒ (cos θ – sin θ)2 = 2 –1
⇒ (cos θ – sin θ)2 = 1
⇒ (cos θ – sin θ) =√1
⇒ (cos θ – sin θ) = ±1




















































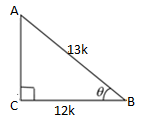










Hamko Hindi Solutions
ReplyDelete